【题目】某商场进了一批台灯,进价为30元,每个以40元卖出时,平均每月能销售600个。调查表明,在一定的售价范围内,售价x和销售量y满足如图的函数关系。
(1)求出销售量y和售价x的函数关系式,并写出自变量的范围;
(2)若平均每月想获得利10000元,则售价应定为多少元?
(3)设每个月的销售利润为w,则将灯的售价定为多少元时,每个月可以获得最大的销售利润?是多少元?

参考答案:
【答案】(1)y=-10x+1000![]() (2)50(3)65,12250
(2)50(3)65,12250
【解析】
试题分析:(1)根据待定系数法,结合图形直接设y=kx+b,然后可求一次函数的解析式及取值范围;
(2)用销售量×单件利润即可得到方程,然后求解即可;
(3)用销售量×单件利润即可得到利润的解析式,然后根据二次函数的最值求解即可.
试题解析:(1)设y=kx+b(k≠0)
则有![]() 解得:
解得:![]()
∴y=-10x+1000![]()
(2)![]()
解得:![]()
∵![]()
∴x取50元
答:若平均每月想获得利10000元,则售价应定为50元。
(3) ![]()
![]()
∵![]()
∴当x=65时,w有最大利润
答:将灯的售价定为65元时,每个月可以获得最大的销售利润12250元。
-
科目: 来源: 题型:
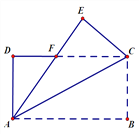
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=8 cm,AD=4 cm,将ΔABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点。
(1)证明:AF=CF;
(2)求ΔAFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将抛物线y=x2﹣4先向右平移两个单位,再向上平移两个单位,得到的抛物线的解析式是( )
A.y=(x+2)2+2
B.y=(x﹣2)2﹣2
C.y=(x﹣2)2+2
D.y=(x+2)2﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上高AD=12,试求△ABC周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形顶角的平分线是一条( )
A. 线段 B. 射线 C. 直线 D. 以上都有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x﹣3的最小值为( )
A.5
B.0
C.﹣3
D.﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)如图2,过A、E、F三点作圆,若EC=4,∠CEF=15°,求AE的长.
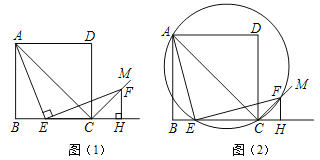
相关试题

