【题目】某商贸公司购进某种水果的成本为20元/千克,经过市场调研发现,这种水果在未来48天的售价p(元/千克)与时间t(天)之间的函数表达式为
p=
且其日销售量y(kg)与时间t(天)的关系如下表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求第30天的日销售量是多少?
(2)问:哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
参考答案:
【答案】(1) 60 kg;(2) 第10天利润最大,最大利润为1250元;(3) 7≤n<9.
【解析】试题分析:(1)设y=kt+b,利用待定系数法即可解决问题.
(2)日利润=日销售量×每公斤利润,据此分别表示前24天和后24天的日利润,根据函数性质求最大值后比较得结论.
(3)列式表示前24天中每天扣除捐赠后的日销售利润,根据函数性质求n的取值范围.
试题解析:
(1)设y=kt+b.
把t=1,y=118;t=3,y=114代入,得![]() 解得
解得![]()
∴y=-2t+120.
当t=30时,y=-2×30+120=60.
∴第30天的日销售量是60 kg.
(2)设第x天的销售利润为w元.
当1≤t≤24时,由题意,得
w=(-2t+120)![]()
=-![]() (t-10)2+1250,
(t-10)2+1250,
∴当t=10时,w最大,为1250.
当25≤t≤48时,
w=(-2t+120)![]()
=t2-116t+3360.
∵对称轴为直线x=58,a=1>0,
∴在对称轴左侧w随t的增大而减小,
∴当t=25时,w最大,为1085.
综上所述,第10天利润最大,最大利润为1250元.
(3)设每天扣除捐赠后的日销售利润为m元.
由题意,得m=(-2t+120)![]() -(-2t+120)n=-
-(-2t+120)n=-![]() t2+(10+2n)t+1200-120n.
t2+(10+2n)t+1200-120n.
∵在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴-![]() ≥24,∴n≥7.
≥24,∴n≥7.
又∵n<9,∴n的取值范围为7≤n<9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角是58°,那么它的补角等于( )
A.22°B.32°C.122°D.132°
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t (h),甲、乙前进的路程与时间的函数图象如图所示.①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是10千米/小时;根据图象信息,下列说法正确的是( )
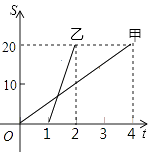
A.①
B.③
C.①②
D.①③ -
科目: 来源: 题型:
查看答案和解析>>【题目】很久很久以前,在古希腊的某个地方发生大旱,地里的庄稼都干死了,人们找不到水喝,于是大家一起到神庙里去向神祈求.神说:“我之所以不给你们降水,是因为你们给我做的正方体祭坛太小,如果你们做一个比它大一倍的祭坛放在我面前,我就会给你们降雨.”大家觉得很好办,于是很快做好了一个新祭坛送到神那里,新祭坛的棱长是原来的2倍.可是神愈发恼怒,他说:“你们竟敢愚弄我.这个祭坛的体积不是原来的2倍,我要进一步惩罚你们!”
如图所示,不妨设原祭坛边长为a,想一想:
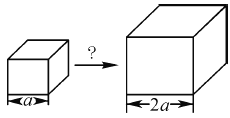
(1)做出来的新祭坛是原来体积的多少倍?
(2)要做一个体积是原来祭坛的2倍的新祭坛,它的棱长应该是原来的多少倍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y1=2x与双曲线y2=
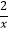 的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<﹣1.”你同意他的观点吗? 答: . 理由是 .
的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<﹣1.”你同意他的观点吗? 答: . 理由是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x+2)(x-2)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校篮球队进行篮球投篮训练,下表是某队员投篮的统计结果:
投篮次数 次
10
50
100
150
200
命中次数 次
9
40
75
108
144
命中率
0.9
0.8
0.75
0.72
0.72
根据上表,你估计该队员一次投篮命中的概率大约是( )
A.0.72B.0.75C.0.8D.0.9
相关试题

