Question

在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝13 cm，BC＝16 cm，CD＝5 cm，AB为⊙O的直径，动点P，沿AD从点A开始向点D以1 cm/s的速度运动，动点Q沿CB从点C开始向点B以2 cm/s的速度运动．点P、Q分别从A、C两点同时出发，当其中一点停止时，另一点也随之停止运动．

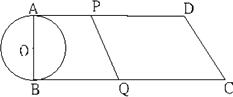
(1)求⊙O的直径；

(2)求四边形PQCD的面积S关于P、Q点运动的时间t的函数关系式，并求出四边形PQCD为等腰梯形时，四边形PQCD的面积；

(3)是否存在某一时刻t，使直线PQ与⊙O相切？若存在，求出t的值；若不存在，说明理由．