【题目】如图,若△ABC和△DEF的面积分别为S1、S2 , 则( ) 
A.S1= ![]() S2
S2
B.S1= ![]() S2
S2
C.S1=S2
D.S1= ![]() S2
S2
参考答案:
【答案】C
【解析】解:过A点作AG⊥BC于G,过D点作DH⊥EF于H. 在Rt△ABG中,AG=ABsin40°=5sin40°,
∠DEH=180°﹣140°=40°,
在Rt△DHE中,DH=DEsin40°=8sin40°,
S1=8×5sin40°÷2=20sin40°,
S2=5×8sin40°÷2=20sin40°.
则S1=S2 .
故选:C.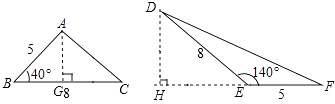
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.
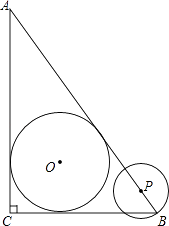
(1)求⊙O的半径;
(2)点P从点B沿边BA向点A以1cm/s的速度匀速运动,以P为圆心,PB长为半径作圆,设点P运动的时间为t s,若⊙P与⊙O相切,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【问题提出】 学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.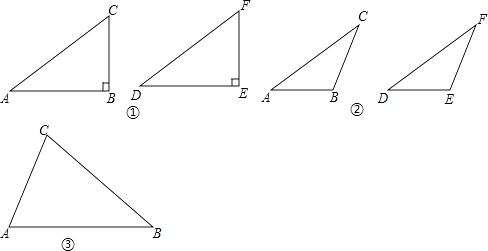
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 , 可以知道Rt△ABC≌Rt△DEF. 第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF. 第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 , 则△ABC≌△DEF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线
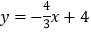 与x轴、y轴分别交于点D、E,交OB于点F.
与x轴、y轴分别交于点D、E,交OB于点F. (1)写出图中的全等三角形及理由;
(2)求OF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行修整改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜,今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”. 最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
品种
产量(斤/每棚)
销售量(元/每斤)
成本(元/每棚)
香瓜
2000
12
8000
甜瓜
4500
3
5000
现假设李师傅今年下半年香瓜种植的大棚数为x个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为y元.
根据以上提供的信息,请你解答下列问题:
(1)求出y与x之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚? 才能使获得的利润不低于10万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】具备下列条件的三角形中,不是直角三角形的是( )
A. ∠A+∠B=∠C B. ∠B=∠C=
 ∠A
∠AC. ∠A=90°-∠B D. ∠A-∠B=90°
-
科目: 来源: 题型:
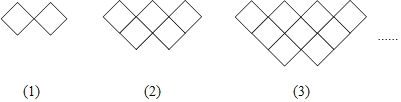
查看答案和解析>>【题目】如图,图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,按此规律,则第(n)个图形中面积为1的正方形的个数为( )
A.
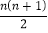 B.
B. 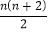 C.
C. 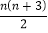 D.
D. 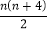
相关试题

