【题目】如图,△ABC中,AB=BC,CD⊥AB于点D,CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G.
(1)求证:△ADC≌△FDB;
(2)求证:CE=![]() BF;
BF;
(3)连结CG,判断△ECG的形状,并说明理由.

参考答案:
【答案】(1)证明见解析 (2)证明见解析 (3)证明见解析
【解析】
(1)首先根据AB=BC,BE平分∠ABC,得到BE⊥AC,CE=AE,进一步得到∠ACD=∠DBF,结合CD=BD,即可证明出△ADC≌△FDB;(2)由△ADC≌△FDB得到AC=BF,结合CE=AE,即可证明出结论;(3)由点H是BC边的中点,得到GH垂直平分BC,即GC=GB,由∠DBF=∠GBC=∠GCB=∠ECF,得∠ECO=45°,结合BE⊥AC,即可判断出△ECG的形状;
证明:(1)∵AB=BC,BE平分∠ABC,
∴BE⊥AC,CE=AE
∵CD⊥AB,
∴∠ACD=∠DBF,
在△ADC和△FDB中,
 ,
,
∴△ADC≌△FDB(ASA);
(2)∵△ADC≌△FDB,
∴AC=BF,
又∵CE=AE,
∴CE=![]() BF;
BF;
(3)△ECG为等腰直角三角形.
∵点H是BC边的中点,
∴GH垂直平分BC,
∴GC=GB,
∵∠DBF=∠GBC=∠GCB=∠ECF,
∵DB=DC,∠BDC=90°,
∴∠ECG=∠DCB=45°,
又∵BE⊥AC,
∴△ECG为等腰直角三角形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在
 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 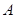 处飞出(
处飞出( 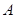 在
在  轴上),运动员孙可在距
轴上),运动员孙可在距  点6米的
点6米的  处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点  ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.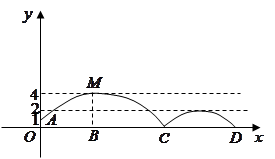
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 距守门员多少米?(取
距守门员多少米?(取  )
)
(3)孙可要抢到足球第二个落地点 ,他应从第一次落地点
,他应从第一次落地点  再向前跑多少米?(取
再向前跑多少米?(取  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,请按照要求解答问题.
(1)数轴上的点C在2、3的正中间位置,则点C表示的数是 ,线段AB的中点D表示的数是 ;
(2)线段AB的中点D与线段BC的中点E的距离为 ;
(3)在数轴上方有一点M,下方有一点N,且∠ABM=120°,∠CBN=60°,请画出示意图,并判断BC是否平分∠MBN.简要说明理由.
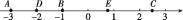
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是具有
 多年历史的古城扬州市区内的几个旅游景点分布示意图. 已知竹西公园的位置坐标为(300,300)(小正方形的边长代表100 m长). 则荷花池的坐标为________;平山堂的坐标为___________;汪氏小苑的坐标为___________.
多年历史的古城扬州市区内的几个旅游景点分布示意图. 已知竹西公园的位置坐标为(300,300)(小正方形的边长代表100 m长). 则荷花池的坐标为________;平山堂的坐标为___________;汪氏小苑的坐标为___________.
-
科目: 来源: 题型:
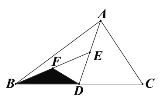
查看答案和解析>>【题目】如图,D、E、F分别为BC、AD、BE的中点,若△BFD的面积为6,则 △ABC的面积等于_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图图形,它是按一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形十字星与五角星的个数和为7,第2个图形十字星与五角星的个数和为10,第3个图形十字星与五角星的个数和为13,按照这样的规律.则第8个图形中,十字星与五角星的个数和为( )

A. 25B. 27C. 28D. 31
相关试题

