【题目】“共享单车”逐渐成为人们方便快捷的出行方式,这些单车投入市场后使用者通过扫描车上二维码注册,首次需对该品牌车辆一次性支付一定数额的押金,而后就可以多次使用该品牌的任意一辆单车,按照使用的次数进行付费。2017年无锡市场上主要有“小鸣”单车、“摩拜”单车、hellobike和ofo小黄车。某公司2017年负责运营“小鸣”单车和摩拜单车,在2017年年初一次性投入700万元购买两种单车投入市场,这些单车投入市场后平均每辆车能收到3位不同使用者支付的押金,共收取押金3585万元。这两种单车的成本、每辆车押金、每辆车平均每天使用的次数、每次使用的价格和每种单车年平均使用率如下表所示:
类型 | 成本 (元/辆) | 押金 (元/辆) | 每辆车平均每天使用的次数 | 每次使用的价格(元/次) | 单车年平均使用率 |
“小鸣”单车 | 120 | 199 | 4 | 1 | 60℅ |
“摩拜”单车 | 170 | 299 | 3 | 2 | 50℅ |
(1)求2017年该公司投入市场的“小鸣”单车、“摩拜”单车各多少万辆?
(2)若这些车投入市场后,该公司所收取的押金每年能稳定在3585万元,所收押金每年还能获取15℅的投资收益,但每辆车每年需要投入35元的维护费,公司每年还需要各项支出725万元,每辆单车按照实际使用200天计算,该公司至少几年后能获得不低于8411万元的利润?
(利润=押金投资收益+单车运营收入-维护费-支出-单车成本)
参考答案:
【答案】(1)“小鸣”单车、“摩拜”单车各3,2万辆.(2)该公司至少4年后能获得不低于8411万元的利润.
【解析】(1)设“小鸣”单车、“摩拜”单车各x,y万辆.由题意列出方程组进而得出等式求出答案;(2)利用不等式求出该公司至少几年后能获得不低于8411万元的利润.
(1)设“小鸣”单车、“摩拜”单车各x,y万辆.
根据题意得:
![]() ;
;
解得![]() ;
;
答:“小鸣”单车、“摩拜”单车各3,2万辆.
(2)设该公司至少n年后能获得不低于8411万元的利润.
(3585![]() 15℅+4
15℅+4![]() 200
200![]() 3
3![]() 60℅+6
60℅+6![]() 200
200![]() 2
2![]() 50℅-5
50℅-5![]() 35-725)n-700≥8411;
35-725)n-700≥8411;
解得:n≥4;
答: 该公司至少4年后能获得不低于8411万元的利润.
“点睛”此题主要考查了二元一次方程组、一元一次不等式的应用,关键是正确理解题意,抓住题目中的关键语句,列出方程组和不等式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M(﹣2,1)关于x轴对称的点的坐标是( )
A.(﹣2,﹣1)
B.(2.1)
C.(2,﹣1)
D.(1.﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,海拔高度每上升1 km,温度下降6 ℃.某时刻测量某市地面温度为20 ℃.设高出地面x km处的温度为y ℃,则y与x的函数关系式为___,y___x的一次函数(填“是”或“不是”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式能用完全平方公式进行分解因式的是( )
A、x2+1B、x2+2x﹣1
C、x2+x+1D、x2+4x+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率给出的统计图如图所示,则符合这一结果的实验可能是( )
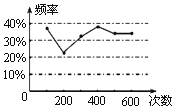
A.掷一枚正六面体的骰子,出现5点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
相关试题

