【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
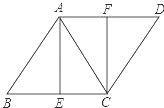
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.
参考答案:
【答案】(1)证明见解析(2)24![]()
【解析】
试题分析:(1)首先证明△ABC是等边三角形,进而得出∠AEC=90°,四边形AECF是平行四边形,即可得出答案;
(2)利用勾股定理得出AE的长,进而求出菱形的面积.
(1)证明:∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC(等腰三角形三线合一),
∴∠AEC=90°,
∵E、F分别是BC、AD的中点,
∴AF=![]() AD,EC=
AD,EC=![]() BC,
BC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形),
又∵∠AEC=90°,
∴四边形AECF是矩形(有一个角是直角的平行四边形是矩形);
(2)解:在Rt△ABE中,AE=![]() =3
=3![]() ,
,
所以,S菱形ABCD=8×3![]() =24
=24![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b互为相反数,c、d互为倒数,x的相反数是它本身,则(a+b)2+cd+x(a+b+c+d)= ___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第三象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )
A. (-4,-3) B. (-3,4) C. (-3,-4) D. (3,-4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值小于5的所有整数的和为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣2≤0的解集是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
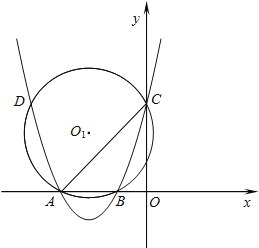
(1)求抛物线的解析式;
(2)求⊙O1的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y=kx(x≥0)与反比例函数y=
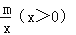 的图象交于点A(2,3),
的图象交于点A(2,3),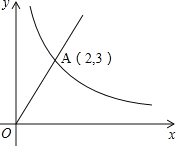
(1)求k,m的值;
(2)写出正比例函数值大于反比例函数值时自变量x的取值范围.
相关试题

