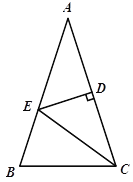
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=12,求BC长.
参考答案:
【答案】(1)36°;(2)5.
【解析】试题分析:(1)、根据中垂线的性质得出∠ECD=∠A;(2)、根据等腰三角形的性质得出∠B=∠ACB=72°,然后得出∠BCE=36°,从而得出∠BEC=72°=∠B,然后得出答案.
试题解析:(1)、∵DE垂直平分AC, ∴CE=AE, ∴∠ECD=∠A=36°.
(2)、∵AB=AC,∠A=36°, ∴∠B=∠ACB=72°,∵∠ECD=36°,∴∠BCE=∠ACB﹣∠ECD=36°,
∠BEC=72°=∠B, ∴BC=EC=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2+bx+1=0有两个不相等的实数根,则a的值可以是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(5,y﹣1),B(x+3,﹣2)分别在第一象限、第三象限内,分别求x、y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣1)×1的结果是( )
A.﹣1
B.0
C.1
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣3,0)和B(1,0),与y轴交于点C,
(1)求抛物线的表达式;
(2)若点D为此抛物线上位于直线AC上方的一个动点,当△DAC的面积最大时,求点D的坐标;
(3)设抛物线顶点关于y轴的对称点为M,记抛物线在第二象限之间的部分为图象G.点N是抛物线对称轴上一动点,如果直线MN与图象G有公共点,请结合函数的图象,直接写出点N纵坐标t的取值范围.
相关试题

