【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.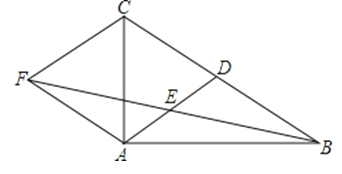
参考答案:
【答案】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中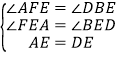
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
(2)四边形ADCF是菱形,
证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,
∴AD=![]() BC=DC,
BC=DC,
∴平行四边形ADCF是菱形.
【解析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案;
(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,P是BC边上除点B、C外的任意一点,则AP2+PBPC= .
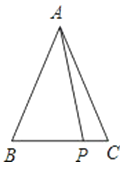
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学初,王刚同学对部分同学暑假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如下表:
时间分组
0.5~20.5
20.5~40.5
40.5~60.5
60.5~80.5
80.5~100.5
频 数
20
25
30
15
10
(1)王刚同学抽取样本的容量是多少?
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线 过点B,C.
过点B,C.(1)求b、c的值;
(2)若点D是抛物线在x轴下方图象上的动点,过点D作x轴的垂线,与直线BC相交于点E.当线段DE的长度最大时,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富校园文化,促进学生全面发展.我市某区教育局在全区中小学开展“书法、武术、黄梅戏进校园”活动。今年3月份,该区某校举行了“黄梅戏”演唱比赛,比赛成绩评定为A,B,C,D,E五个等级,该校部分学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图,请根据图中信息,解答下列问题.

(1)求该校参加本次“黄梅戏”演唱比赛的学生人数;
(2)求扇形统计图B等级所对应扇形的圆心角度数;
(3)已知A等级的4名学生中有1名男生,3名女生,现从中任意选取2名学生作为全校训练的示范者,请你用列表法或画树状图的方法,求出恰好选1名男生和1名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用一副三角板上已知度数的角,不能画出的角是( )
A.15°
B.135°
C.165°
D.100° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a>0)的对称轴是直线x=2,且经过点P(3,1),则a+b+c的值为____________.
相关试题

