【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=﹣![]() x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.

(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
参考答案:
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)﹣1<x<3.
x+2;(2)﹣1<x<3.
【解析】
试题分析:(1)根据正方形的性质得出点B、C的坐标,然后利用待定系数法求函数解析式解答;
(2)令y=0求出二次函数图象与x轴的交点坐标,再根据y>0,二次函数图象在x轴的上方写出x的取值范围即可.
解:(1)∵正方形OABC的边长为2,
∴点B、C的坐标分别为(2,2),(0,2),
∴ ,
,
解得![]() ,
,
∴二次函数的解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)令y=0,则﹣![]() x2+
x2+![]() x+2=0,
x+2=0,
整理得,x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
∴二次函数与x轴的交点坐标为(﹣1,0)、(3,0),
∴当y>0时,x的取值范围是﹣1<x<3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).

(1)小明的这三件文具中,可以看做是轴对称图形的是 (填字母代号);
(2)小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=
 AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
A.①② B.②③ C.①③ D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的面积为10cm2,它的两条对角线交于,点O1以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )
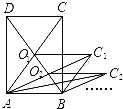
A.10cm2 B.
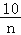 cm2 C.
cm2 C.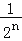 cm2 D.
cm2 D.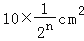
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动.给出以下四个结论:

①AE=AF;
②∠CEF=∠CFE;
③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;
④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.
上述结论中正确的序号有 .(把你认为正确的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AB=34,并且AC:BC=8:15,则AC=__,BC=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加快镇康经济社会发展,促进区域资源开发,巩固国防维护边境稳定,2016 年 11 月镇康县(南伞)至孟定(清水河)高速公路段可行性研究报告通过省发改委批复,预计总投资 55 亿余元,55 亿用科学记数法表示为__________元.
相关试题

