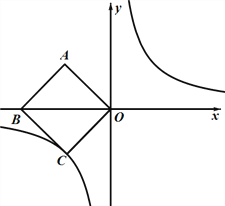
【题目】如图,在平面直角坐标系![]() 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为![]() ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数![]() 的图象经过C点.
的图象经过C点.
(1)求该反比例函数的解析式;
(2)当函数值![]() >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;
(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
参考答案:
【答案】(1)![]() ;(2)x<-2或x>0 (3)(1,4)或(﹣1,﹣4).
;(2)x<-2或x>0 (3)(1,4)或(﹣1,﹣4).
【解析】分析:(1)利用正方形边长和正方形位置特点,可求得C点坐标,待定系数法求反比例函数解析式.(2)利用反比例函数与不等式的关系,数形结合求不等式.(3)利用面积相等,列方程,求解P点坐标.
详解:(1)AO=![]() ,根据勾股定理知,BO=4,所以C(-2,-2), 反比例函数
,根据勾股定理知,BO=4,所以C(-2,-2), 反比例函数![]() 的图象经过C点,
的图象经过C点,
所以![]() =-2,k=4.
=-2,k=4. ![]() .
.
(2)画出y=-2,数形结合知,x<-2或x>0

(3)设P(x, ![]() ,所以S△PBO=SABCO,
,所以S△PBO=SABCO,
![]() =AO2,
=AO2,
![]() ,x=
,x=![]() ,
,
所以P(1,4)或(﹣1,﹣4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
 若一元二次方程
若一元二次方程 有一个根是
有一个根是 ,则代数式
,则代数式 的值是
的值是
 若
若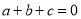 ,则
,则 是一元二次方程
是一元二次方程 的一个根
的一个根 若
若 ,则一元二次方程
,则一元二次方程 有不相等的两个实数根
有不相等的两个实数根 当m取整数
当m取整数 或1时,关于x的一元二次方程
或1时,关于x的一元二次方程 与
与 的解都是整数.
的解都是整数.其中正确的有

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
①(+12)+(-4)=______ ②(-5)+5=________
③(-2)-(-2)=_______ ④ 0-3=________
⑤(-3)+(-6)=_______ ⑥ (-6)+(+4)=________
⑦
 =_______ ⑧(-0.2)-(-
=_______ ⑧(-0.2)-(-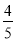 )_______
)_______⑨
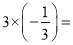 _______
_______ -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中
 如图
如图 ,已知抛物线
,已知抛物线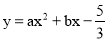 ,经过点
,经过点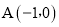 、
、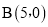 .
.
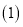 求此抛物线顶点C的坐标;
求此抛物线顶点C的坐标; 联结AC交y轴于点D,联结BD、BC,过点C作
联结AC交y轴于点D,联结BD、BC,过点C作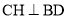 ,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点,以AD为边在AD的右侧作正方形ADEF.
(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的关系为 ;
(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?请说明理由;
(3)设D点坐标为(t,0),当D点从O点运动到C点时,用含t的代数式表示E点坐标,求出E点所满足的函数关系式,并写出E点所经过的路径长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=BD=4,E为AB的中点,P为AC上一个动点,则EP+BP的最小值为_____.

相关试题

