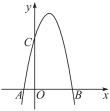
【题目】如图,一个二次函数的图象经过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴的正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
参考答案:
【答案】(1)点C的坐标为(0,5);(2)所求二次函数的解析式为y=-![]() x2+
x2+![]() x+5,最大值为
x+5,最大值为![]() .
.
【解析】
(1)根据A.B两点的坐标及点C在y轴正半轴上,且AB=OC.求出点C的坐标为(0,5);
(2)设二次函数的解析式为y=ax2+bx+c,把A、B、C三点的坐标代入解析式,可求出a、b、c的值.
(1)∵A(-1,0),B(4,0)
∴AO=1,OB=4,
AB=AO+OB=1+4=5,
∴OC=5,即点C的坐标为(0,5);
(2)设图象经过A、C、B三点的二次函数的解析式为y=ax2+bx+c
由于这个函数图象过点(0,5),可以得到C=5,又由于该图象过点(-1,0),(4,0),则:
![]() ,
,
解方程组,得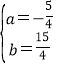
∴所求的函数解析式为y=-![]() x2+
x2+![]() x+5
x+5
∵a=-![]() <0
<0
∴当x=-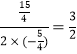 时,y有最大值
时,y有最大值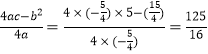 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=ax
 +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x -3x+5,则a+b+c=__________。
-3x+5,则a+b+c=__________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC.点D从点B出发沿射线BC移动,以AD为边在AB的右侧作△ADE,且∠DAE=90°,AD=AE.连接CE.
(1)如图1,若点D在BC边上,则∠BCE=______度;
(2)如图2,若点D在BC的延长线上运动.
①∠BCE的度数是否发生变化?请说明理由;
②若BC=6,CD=2,求△ADE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把抛物线y=
 x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
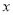 的函数
的函数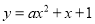 (
(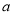 为常数)
为常数)(1)若函数的图象与
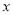 轴恰有一个交点,求
轴恰有一个交点,求 的值;
的值;(2)若函数的图象是抛物线,且顶点始终在
 轴上方,求
轴上方,求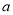 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于
 EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
A. 120° B. 30° C. 150° D. 60°
-
科目: 来源: 题型:
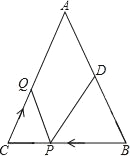
查看答案和解析>>【题目】如图,在△ABC中,∠B=∠C,AB=8,BC=6,点D为AB的中点,点P在线段BC上以每秒2个单位的速度由点B向点C运动,同时点Q在线段CA上以每秒a个单位的速度由点C向点A运动,设运动时间为t(秒)(0≤t≤3).
(1)用含t的代数式表示线段PC的长;
(2)若点P、Q的运动速度相等,t=1时,△BPD与△CQP是否全等,请说明理由.
(3)若点P、Q的运动速度不相等,△BPD与△CQP全等时,求a的值.
相关试题

