【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
参考答案:
【答案】
(1)解:如图所示,△A1B1C1为所求做的三角形;
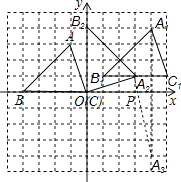
(2)解:如图所示,△A2B2O为所求做的三角形;

(3)解:∵A2坐标为(3,1),A3坐标为(4,﹣4),
∴A2A3所在直线的解析式为:y=﹣5x+16,
令y=0,则x= ![]() ,
,
∴P点的坐标( ![]() ,0).
,0).
【解析】本题考查了利用旋转和平移变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.(1)分别将点A、B、C向上平移1个单位,再向右平移5个单位,然后顺次连接;(2)根据网格结构找出点A、B、C以点O为旋转中心顺时针旋转90°后的对应点,然后顺次连接即可;(3)利用最短路径问题解决,首先作A1点关于x轴的对称点A3 , 再连接A2A3与x轴的交点即为所求.
-
科目: 来源: 题型:
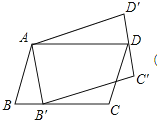
查看答案和解析>>【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)(﹣2,1),先将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2 , 点A1的对应点为点A2 .
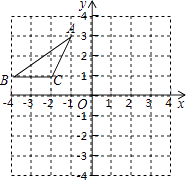
(1)画出△A1B1C1;
(2)画出△A2B2C2;
(3)求出在这两次变换过程中,点A经过点A1到达A2的路径总长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.

(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2的单位,这种点的运动称为点A的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5),已知点A的坐标为(1,0).

(1)分别写出点A经1次,2次斜平移后得到的点的坐标.
(2)如图,点M是直线l上的一点,点A关于点M的对称点的点B,点B关于直线l的对称轴为点C.
①若A、B、C三点不在同一条直线上,判断△ABC是否是直角三角形?请说明理由.
②若点B由点A经n次斜平移后得到,且点C的坐标为(7,6),求出点B的坐标及n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C是反比例函数y=
 (k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )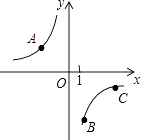
A.4条
B.3条
C.2条
D.1条
相关试题

