【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF的值。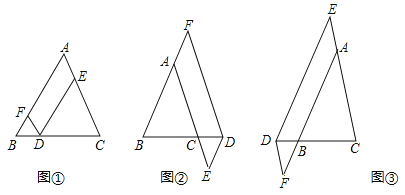
参考答案:
【答案】解:(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∴AF=DE,
∵DF∥AC,
∴∠FDB=∠C
又∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B
∴DF=BF
∴DE+DF=AB=AC;
(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC﹣DE=6﹣4=2;
当如图②的情况,DF=AC+DE=6+4=10.
故答案是:2或10.
【解析】(1)证明四边形AFDE是平行四边形,且△DEC和△BDF是等腰三角形即可证得;
(2)与(1)的证明方法相同;
(3)根据(1)(2)中的结论直接求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年1月25日健康网报道,截止到2015年12月,中国有网民6.88亿人,其中学生比例最高,为25.2%,人均每周上网26.2小时,某校为了解本校七年级800名学生每天上网的情况,王老师随机调查统计了若干名学生平均每天的上网时间,并将统计结果进行分组(每组含最小值,不含最大值):A组:0﹣0.5小时;B组:0.5﹣1小时;C组:1﹣1.5小时;D组:1.5﹣2小时;E组:2﹣2.5小时.分组后绘制成如图1所示的不完整的统计图.

(1)写出本次调查的总体;
(2)补全频数分布直方图和扇形统计图;
(3)求图2中A组所对的扇形的圆心角的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】线段CD是由线段AB平移得到的.点A(﹣1,4)的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的坐标为( )
A.(2,9)
B.(5,3)
C.(1,2)
D.(﹣9,﹣4) -
科目: 来源: 题型:
查看答案和解析>>【题目】继2017年北仓区经济总量迈上1000亿元的新台阶,2018年再创新高,全年生产总值约1147亿元,1147亿用科学记数法表示为( )
A. 1.147×108B. 1.147×109C. 1.147×1010D. 1.147×1011
-
科目: 来源: 题型:
查看答案和解析>>【题目】武汉某天冬季的最高气温9℃,最低气温﹣3℃,这一天武汉最高气温比最低气温高( )
A. 12℃ B. ﹣12℃ C. 6℃ D. ﹣6℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条河的水流速度是1.8km/h,某条船在静水中的速度是akm/h,则该船在这条河中逆流行驶的速度是( )
A. (a+1.8)km/h B. (a﹣1.8)km/h
C. (a+3.6)km/h D. (a﹣3.6)km/h
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.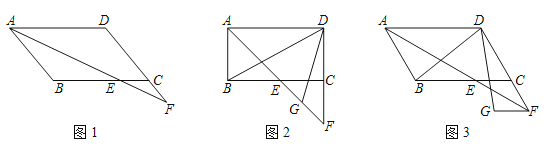
相关试题

