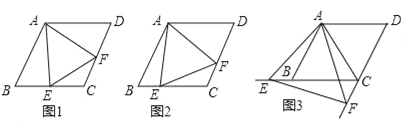
【题目】(2016广西省南宁市第23题)已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
参考答案:
【答案】(1)、AE=EF=AF;(2)、证明过程见解析;(3)、3-![]()
【解析】
试题分析:(1)、结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形;(2)、欲证明BE=CF,只要证明△BAE≌△CAF即可;(3)、过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CFcos30°,因为CF=BE,只要求出BE即可解决问题.
试题解析:(1)、结论AE=EF=AF.
理由:如图1中,连接AC, ∵四边形ABCD是菱形,∠B=60°, ∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形, ∴∠BAC=∠DAC=60° ∵BE=EC, ∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°, ∴∠CAF=∠DAF=30°, ∴AF⊥CD, ∴AE=AF(菱形的高相等),
∴△AEF是等边三角形, ∴AE=EF=AF.
(2)、如图2中,∵∠BAC=∠EAF=60°, ∴∠BAE=∠CAE,
在△BAE和△CAF中,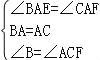 , ∴△BAE≌△CAF, ∴BE=CF.
, ∴△BAE≌△CAF, ∴BE=CF.
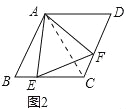
(3)、过点A作AG⊥BC于点G,过点F作FH⊥EC于点H, ∵∠EAB=15°,∠ABC=60°, ∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°AB=4, ∴BG=2,AG=2![]() ,在RT△AEG中,∵∠AEG=∠EAG=45°,
,在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2![]() , ∴EB=EG﹣BG=2
, ∴EB=EG﹣BG=2![]() ﹣2, ∵△AEB≌△AFC,
﹣2, ∵△AEB≌△AFC,
∴AE=AF,EB=CF=2![]() ﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等边三角形,
﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等边三角形,
∴∠AEF=∠AFE=60° ∵∠AEB=45°,∠AEF=60°, ∴∠CEF=∠AEF﹣∠AEB=15°,
在RT△EFH中,∠CEF=15°, ∴∠EFH=75°, ∵∠AFE=60°, ∴∠AFH=∠EFH﹣∠AFE=15°,
∵∠AFC=45°,∠CFH=∠AFC﹣∠AFH=30°, 在RT△CHF中,∵∠CFH=30°,CF=2![]() ﹣2,
﹣2,
∴FH=CFcos30°=(2![]() ﹣2)
﹣2)![]() =3﹣
=3﹣![]() . ∴点F到BC的距离为3﹣
. ∴点F到BC的距离为3﹣![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a2=a6
B.a3+a2=2a5
C.(2a2)3=2a6
D.2a6÷a2=2a4 -
科目: 来源: 题型:
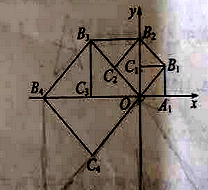
查看答案和解析>>【题目】(2016山东省聊城市第17题)如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(x , y)关于原点的对称点为(-2,3),则x+y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】记M(1) = -2,M(2) =(-2)×(-2),M(3) = (-2)×(-2) ×(-2),……,
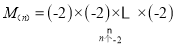
(1)填空:M(5) = ,分析M(50) =是一个 数(填“正”或“负”)
(2)计算M(6) + M(7) ;
(3)当M(n) <0时,直接写出2016 M(n) +1008M(n+1)的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x(x﹣5)=0的解是( ).
A. 0 B. 5 C. 0和5 D. 0和﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式4a2b+4ab2+b3因式分解正确的是( )
A.a(2a+b)2B.b(2a+b)2C.(a+2b)2D.4b(a+b)2
相关试题

