【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB绕点O逆时针旋转90°后得到△A1OB1 . 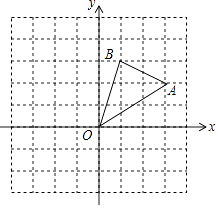
(1)点A关于点O中心对称的点P的坐标为;
(2)在网格内画出△A1OB1;
(3)点A1、B1的坐标分别为 .
参考答案:
【答案】
(1)(﹣3,﹣2)
(2)
解:如图,△A1OB1即为所求
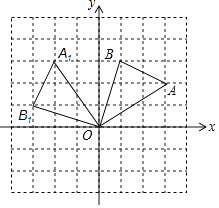
(3)(﹣2,3),(﹣3,1)
【解析】解:(1)∵A(3,2),
∴P(﹣3,﹣2).
所以答案是:(﹣3,﹣2);
(3)由图可知,A1(﹣2,3),B1(﹣3,1).
所以答案是:(﹣2,3),(﹣3,1).
【考点精析】掌握图形的旋转和旋转的性质是解答本题的根本,需要知道每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点
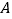 表示
表示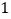 ,现将点
,现将点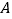 沿
沿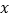 轴做如下移动,第一次点
轴做如下移动,第一次点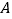 向左移动
向左移动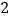 个单位长度到达点
个单位长度到达点 ,第二次将点
,第二次将点 ,向右移动
,向右移动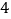 个单位长度到达点
个单位长度到达点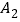 ,第三次将点
,第三次将点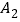 向左移动
向左移动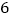 个单位长度到达点
个单位长度到达点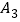 ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第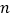 次移动到点
次移动到点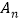 ,如果点
,如果点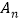 与原点的距离等于
与原点的距离等于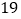 ,那么
,那么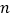 的值是________.
的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并回答问题:
三峡之最
三峡工程是中国,也是世界上最大的水利枢纽工程,是治理和开发长江的关键性骨干工程.它具有防洪、发电、航运等综合效益.
三峡水库总库容
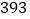 亿立方米,防洪库容
亿立方米,防洪库容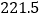 亿立方米,水库调洪可消减洪峰流量达每秒
亿立方米,水库调洪可消减洪峰流量达每秒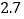 ─
─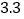 万立方米,是世界上防洪效益最为显著的水利工程.
万立方米,是世界上防洪效益最为显著的水利工程.三峡水电站总装机
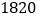 万千瓦,年发电量
万千瓦,年发电量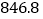 亿千瓦.时,是世界上最大的电站.
亿千瓦.时,是世界上最大的电站.三峡水库回水可改善川江
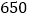 公里的航道,使宜渝船队吨位由现在的
公里的航道,使宜渝船队吨位由现在的 吨级堤高到万吨级,年单向通过能力由
吨级堤高到万吨级,年单向通过能力由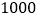 万吨增加到
万吨增加到 万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.思考:
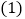 三峡水电站年发电量
三峡水电站年发电量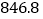 亿千瓦.时,一个普通家庭一天用电
亿千瓦.时,一个普通家庭一天用电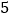 千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留
千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留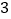 个有效数字)
个有效数字) 宜都市
宜都市 万人,平均一户
万人,平均一户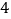 个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B、C在数轴上对应的数为
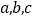 ,且
,且 ,多项式
,多项式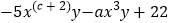 是关于字母x,y的五次多项式.
是关于字母x,y的五次多项式.(1)则a=__,b=__,c=__;并将这三数在数轴上所对应的点A、B、C表示出来;
(2)已知蚂蚁从A点出发,以每秒2cm的速度爬行,先到B点,再到C点,一共需要多少秒?
(3)数轴上在B点右边有一点D到A、B两点的距离和为11,求点D的数轴上所对应的数;(直接写出结果)
(友情提示:M、N之间距离记作|MN|,点M、N在数轴上对应的数分别为m、n,则
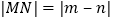 )
)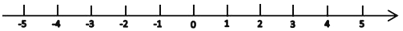
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个可以自由转动的转盘被平均分成4个扇形,分别标有1、2、3、4四个数字,小王和小李各转动一次转盘为一次游戏.当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
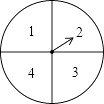
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏结束得到的一组数恰好是方程x2﹣4x+3=0的解的概率.
相关试题

