【题目】如图,已知:Rt△ACB,BC=3,AC=4,延长BC至D,使得△ABD为等腰三角形,求CD的长。
参考答案:
【答案】2;3; ![]()
【解析】试题分析:分三种情况①当AD=AB时,容易得出CD的长;
②当AD=BD时,设CD=x,则AD=x+3,由勾股定理得出方程,解方程即可;
③当BD=AB时,由勾股定理求出AB,即可得出CD的长.
试题解析:分三种情况:
①当AD=AB时,
如图1所示:
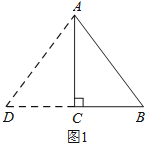
则CD=BC=3;
②当AD=BD时,
如图2所示:
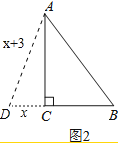
设CD=x,则AD=x+3,
在Rt△ADC中,由勾股定理得:
(x+3)2=x2+42,
解得:x=![]() ,
,
∴CD=![]() ;
;
③当BD=AB时,
如图3所示:
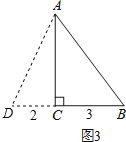
在Rt△ABC中,AB=![]() =5,
=5,
∴BD=5,
∴CD=5-3=2;
综上所述:CD的长为3或![]() 或2;
或2;
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣1)2+2的对称轴是( )
A.直线x=2
B.直线x=﹣2
C.直线x=1
D.直线x=﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的底角为70度,则它的顶角为 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=
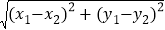 ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为-1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
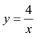 .
.(1) 若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2) 如图,反比例函数
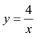 (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移至C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移至C2处所扫过的面积.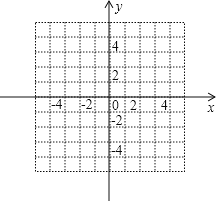
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1=35°21′,则∠1的余角是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x=6是方程2x+3a=6x的解,那么a的值是 .
相关试题

