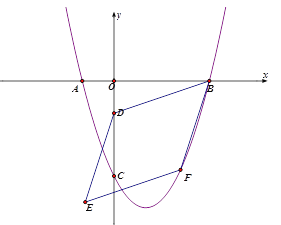
【题目】如图，在平面直角坐标系中，点A在x轴的负半轴上，B点坐标为(6，0)，点C在y轴的负半轴上，且OB=OC，抛物线y=x2+bx+c经过A、B、C三点．

(1)求此抛物线的函数关系式和点A的坐标；

(2)点D的坐标为（0，-2），F为该二次函数图像上的动点，连接BD、BF，以BD、BF为邻边作平行四边形BDEF，

①若点F为该二次函数在第四象限图像上的动点，设平行四边形BDEF的面积为S。求S的最大值。

②在点F的运动过程中，当点E落在一次函数y=x+7上时，求点F的坐标。

参考答案：

【答案】（1）y=x2-x-6 ； A(-3，0)；(2)①32；②F1（-3，0）F2（9，12）

【解析】试题分析：（1）由OC＝OB可得点C的坐标为（0，－6），再将点B、C的坐标代入抛物线y=x2+bx+c中，即可得出抛物线的解析式，当y=0 时，求得x1=-3，x2=6,即点A的坐标为（－3，0）；

（2）①连接OF、DF，设点F的坐标为（t, 2-t-6），根据S四边形OBFD=S△OBD+S△BDF=SODF+S△OBF求得＝－（t-2）2+16，由四边形BDEF是平行四边形得＝，所以当面积最大时，平行四边形BDEF的面积为S也有最大值.由＝－（t-2）2+16得：当t=2时，S△BDF有最大值＝16，即平行四边形BDEF的面积S的最大值 为32.

②设E点坐标为（m,m+7），由BD//EF，且BD=EF，则由D（0，-2）平移到B（6，0），则点E（m,m+7）平移到F（m+6,m+9）,将F（m+6,m+9）代入y=x2-x-6得m+9= (m+6)2-(m+6)-6,即可求得m的值，即可求得F的坐标；

试题解析：

（1）∵OB=OC，B点坐标为(6，0)，

∴点C坐标为（0，－6），

∵点B、C在抛物线y=x2+bx+c上，

∴

解得 ，

∴抛物线的解析式为：y=x2-x-6

当y=0时，即x2-x-6 ＝0，解得x1=-3，x2=6，

所以A(-3，0) .

(2) ①连接OF、DF，如图所示：

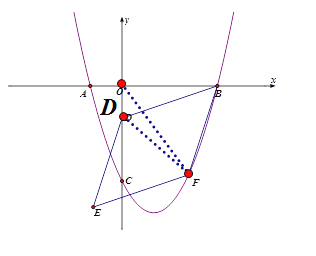
设点F的坐标为（t, 2-t-6）,

∴S△OBD+S△BDF = ,

SODF+S△OBF=

又∵S四边形OBFD=S△OBD+S△BDF=SODF+S△OBF

∴＝，即＝＝－（t-2）2+16

∵四边形BDEF是平行四边形，

∴＝，

∴当面积最大时，平行四边形BDEF的面积为S也有最大值.

当t=2时，S△BDF有最大值＝16，

∴平行四边形BDEF的面积S的最大值 为32.

当x=2时，S的最大值为32

②设E点坐标为（m,m+7）,

∵BD//EF，且BD=EF，则由D（0，-2）平移到B（6，0），

∴点E（m,m+7）平移到F（m+6,m+9）,

将F（m+6,m+9）代入y=x2-x-6得m+9= (m+6)2-(m+6)-6,

解得：m1=-9,m2=3,

所以F1（-3，0）或F2（9，12）.

关闭