【题目】关于x的方程kx2+(k+2)x+ ![]() =0有两个不相等的实数根;
=0有两个不相等的实数根;
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:由△=[(k+2)]2﹣4×k ![]() >0,
>0,
∴k>﹣1
又∵k≠0,
∴k的取值范围是k>﹣1,且k≠0
(2)解:不存在符合条件的实数k
理由:设方程kx2+(k+2)x+ ![]() =0的两根分别为x1、x2,
=0的两根分别为x1、x2,
由根与系数关系有:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
又∵ ![]() +
+ ![]() =
= ![]() =0,
=0,
∴ ![]() =0,
=0,
解得k=﹣2,
由(1)知,k=﹣2时,△<0,原方程无实解,
∴不存在符合条件的k的值.
【解析】(1)由于x的方程kx2+(k+2)x+ ![]() =0有两个不相等的实数根,由此可以得到判别式是正数,这样就可以得到关于k的不等式,解不等式即可求解;(2)不存在符合条件的实数k.设方程kx2+(k+2)x+
=0有两个不相等的实数根,由此可以得到判别式是正数,这样就可以得到关于k的不等式,解不等式即可求解;(2)不存在符合条件的实数k.设方程kx2+(k+2)x+ ![]() =0的两根分别为x1、x2 , 由根与系数关系有:x1+x2=﹣
=0的两根分别为x1、x2 , 由根与系数关系有:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,又
,又 ![]() +
+ ![]() =
= ![]() ,然后把前面的等式代入其中即可求k,然后利用(1)即可判定结果
,然后把前面的等式代入其中即可求k,然后利用(1)即可判定结果
【考点精析】利用求根公式和根与系数的关系对题目进行判断即可得到答案,需要熟知根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同一平面内如果两条直线不重合,那么他们( )
A. 平行B. 相交C. 相交或垂直D. 平行或相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场中,一件夹克衫按成本价提高
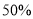 后标价,后为了促销按标价的8折出售,每件240元卖出.
后标价,后为了促销按标价的8折出售,每件240元卖出. 这种夹克衫每件的成本价是多少元?
这种夹克衫每件的成本价是多少元? 这种夹克衫的利润率是多少?
这种夹克衫的利润率是多少? -
科目: 来源: 题型:
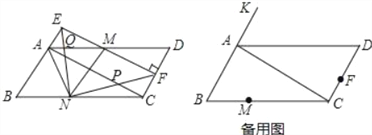
查看答案和解析>>【题目】如图,已知ABCD中,BC=8cm,CD=4cm,∠B=60°,点E从点A出发,沿BA方向匀速运动,速度为1cm/s.过点E作EF⊥CD,垂足是F,连接EF交AD于点M,过M作MN∥AB,MN与BC交于点N,设运动时间为t(s)(0<t<4)
(1)用含t的代数式表示线段AM的长:AM= ;
(2)是否存在某一时刻t,使EN⊥BC,求出相应的t值,若不存在,说明理由;
(3)设四边形AEFN的面积为y(cm2),求y与t之间的函数关系式;
(4)点P是AC与NF的交点,在点E的运动过程中,是否存在某一时刻t,使∠MNP=45°?若存在,求出相应的t值,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和10元;从B校调运一台电脑到C校和D校的运费分别为30元和20元.
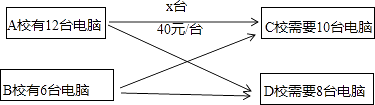
(1)设A校运往C校的电脑为x台,请仿照下图,求总运费W(元)关于x的函数关系式;
(2)求出总运费最低的调运方案,最低运费是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
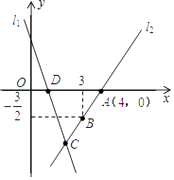
(1)求直线l2的解析表达式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线被第三条直线所截,若∠1与∠2 是同旁内角,且∠1=70,则 ( )
A. ∠2=70B. ∠2=110
C. ∠2=70或∠2=110D. ∠2的度数不能确定
相关试题

