【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.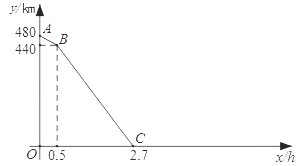
(1)由图象知,慢车的速度为km/h,快车的速度为km/h;
(2)请在图中补全函数图象;
(3)求当x为多少时,两车之间的距离为300km.
参考答案:
【答案】
(1)80,120
(2)解:如图所示:
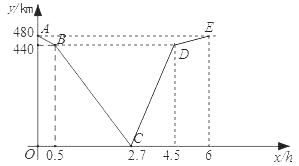
(3)解: 由题意,可知两车行驶的过程中有2次两车之间的距离为300km.
即(80+120)×(x-0.5)=440-300,解得x=1.2(h);(8分)
或(80+120)×(x-2.7)=300,解得x=4.2(h).(10分)故x=1.2 h或4.2h,两车之间的距离为300km
【解析】(1)根据AB段可以确定先出发的车的速度,然后根据BC段确定两车速度的和,则后出发的车的速度可以求得;
(2)根据路程是480km,则可以求得两辆车到达时的时间,然后求得各组到达的所需要的时间,再求得相距的距离即可确定;
(3)两车之间的距离是300km时有两个位置,分成相遇前和相遇后两种情况讨论即可列方程求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若当x=﹣2018时,式子ax3﹣bx﹣3的值为5,则当x=2018时,式子ax3﹣bx﹣3的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果n边形的内角和是它外角和的4倍,则n等于( )
A. 7 B. 8 C. 10 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).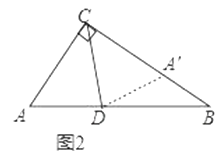
请回答:
(1)在图2中,小明得到的全等三角形是△≌△;
(2)求BC和AC、AD之间的数量关系是
(3)参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.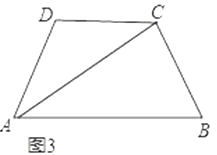
-
科目: 来源: 题型:
查看答案和解析>>【题目】0的相反数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“We like maths.”这个句子的所有字母中,字母“e”出现的频数是( )
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一边长等于6,另一边长等于4,则它的周长等于( )
A. 15 B. 16 C. 14 D. 14或16
相关试题

