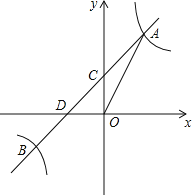
【题目】如图,反比例函数![]() 的图象与一次函数y=kx+b的图象交于点A、B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
的图象与一次函数y=kx+b的图象交于点A、B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)在第三象限的反比例图象上是否存在一个点P,使得S△ODP=2S△OCA?若存在,请求出来P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x+1;(2)-2<x<0;(3)P(-1,-2).
【解析】试题分析:(1)由点A、B的横坐标分别为1,-2,求得A(1,2),B(-2,-1),由于点A、B在一次函数y=kx+b的图象上,列方程组即可得到结论;
(2)根据图象即可得到结论;
(3)存在,根据一次函数的解析式得到D(-1,0),C(0,-1),设P(m,n),根据S△ODP=2S△OCA,列方程即可得到结论.
试题解析:(1)∵点A、B的横坐标分别为1,-2,
∴y=2,或y=-1,
∴A(1,2),B(-2,-1),
∵点A、B在一次函数y=kx+b的图象上,
∴![]() ,
,
∴![]() ,
,
∴一次函数的解析式为:y=x+1;
(2)由图象得知:y<-1时,写出x的取值范围是-2<x<0;
(3)存在,
对于y=x+1,当y=0时,x=-1,当x=0时,y=1,
∴D(-1,0),C(0,1),
设P(m,n),
∵S△ODP=2S△OCA,
∴![]() ×1(-n)=2×
×1(-n)=2×![]() ×1×1,
×1×1,
∴n=-2,
∵点P在反比例图象上,
∴m=-1,
∴P(-1,-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系内,点P(-2,3)关于原点的对称点Q的坐标为( )
A. (2,-3) B. (2,3) C. (-2,3) D. (-2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分,跑步的平均速度为210米/分,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为( )
A. 210x+90(15﹣x)≥1.8B. 90x+210(15﹣x)≤1800
C. 210x+90(15﹣x)≥1800D. 90x+210(15﹣x)≤1.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式(a2+2ab﹣b2)﹣(a2+mab+2b2)中不含ab项,则m=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小镇在2017年常住人口达到25.8万,用科学记数法表示应为( )
A. 25.8×104 B. 25.8×105 C. 2.58×105 D. 2.58×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不可能成为一个三角形三边长的是( )
A.2,4,5B.6,7,7,C.6,8,10D.4,6,12
-
科目: 来源: 题型:
查看答案和解析>>【题目】若n为正整数,则化简(-1)2 na+(-1)2 n+1a的结果是( )
A、0 B、2a C、-2a D、2a或-2a
相关试题

