【题目】如图，等边三角形内接于，点是上两点，且，若，则图中阴影部分的面积为_____．

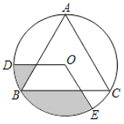
【答案】

【解析】

连接OB，OC，过点O作OH⊥BC于点H，易得：扇形OBD与扇形OCE全等，OBM OCN，进而得到：阴影部分的面积=弓形BEC的面积，根据扇形的面积公式和三角形的面积公式，即可求解.

连接OB，OC，过点O作OH⊥BC于点H，如图，

∵等边三角形内接于，点是上两点，

∴∠BOC=2∠BAC=2×60°=120°，∠OBC=∠OCB=30°，

∴OH=，BC=2BH=2，

∵，

∴∠BOC-∠BOE=∠DOE-∠BOE，即：∠BOD=∠COE，

∴扇形OBD与扇形OCE全等，

在OBM和OCN中，

∵，

∴OBM OCN(AAS)，

∴阴影部分的面积=弓形BEC的面积=，

故答案是：.

关闭