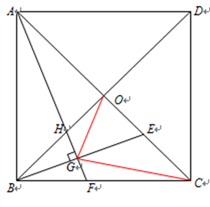
【题目】如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点(与点O不重合)，作AF⊥BE，垂足为G，交BC于F，交B0于H，连接OG，CC．

(1)求证：AH=BE；

(2)试探究：∠AGO的度数是否为定值?请说明理由；

(3)若OG⊥CG，BG=，求△OGC的面积．

【答案】(1)见解析;(2)见解析;(3).

【解析】分析：（1）通过证明△AOH ≌ △BOE得到结论；

（2）易证△AOH∽△BGH得，由∠OHG =∠AHB可得△OHG∽△AHB，从而∠AGO=∠ABO=45°，从而可得结论；

（3）易证△ABG ∽△BFG得,故AG·GF=BG 2 =5.再证明△AGO ∽△CGF.可得GO·CG =AG·GF=5.故S△OGC =CG·GO=.

详解：（1）∵四边形ABCD是正方形,

∴OA=OB，∠AOB=∠BOE=90°

∵AF⊥BE,

∴∠GAE+∠AEG=∠OBE+∠AEG=90°.

∴∠ GAE =∠OBE .

∴△AOH ≌ △BOE.

∴AH=BE .

（2）∵∠AOH=∠BGH=90°, ∠AHO=∠BHG,

∴△AOH∽△BGH.

∴.

∴.

∵∠OHG =∠AHB.

∴△OHG∽△AHB.

∴∠AGO=∠ABO=45°,即∠AGO的度数为定值.

（3）∵∠ABC=90°,AF⊥BE,

∴∠BAG=∠FBG,∠AGB=∠BGF=90°,

∴△ABG ∽△BFG.

∴,

∴AG·GF=BG 2 =5.

∵△AHB∽△OHG，

∴∠BAH=∠GOH=∠GBF.

∵∠AOB=∠BGF=90°,

∴∠AOG=∠GFC.

∵∠AGO=45°,CG⊥GO,

∴∠AGO=∠FGC=45°.

∴△AGO ∽△CGF.

∴,

∴GO·CG =AG·GF=5.

∴S△OGC =CG·GO=.

关闭