【题目】在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象。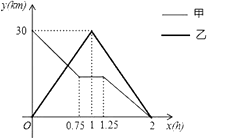
(1)A、B两地间的距离为km;
(2)求乙与B地的距离y(km)与乙行驶时间x(h)之间的函数关系式;
(3)求甲、乙第一次相遇的时间;
(4)若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请求出乙在行进中能用无线对讲机与甲保持联系的x取值范围。
参考答案:
【答案】
(1)30
(2)设乙前往A地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙1=k1x,由题意,得
30=k1,
∴y乙1=30x
设乙返回B地距离B地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙2=k2x+b2,由题意,得![]()
解得:![]()
所以y=-30x+60
(3)由函数图象,得
(30+20)x=30,
解得x=0.6.
∴甲、乙第一次相遇是在出发后0.6小时
(4)
甲在修车前y与x之间的函数关系式为y甲1=kx+b,由题意,得;![]()
解得:![]()
y甲1=-20x+30,
设甲在修车后y与x之间的函数关系式为y甲2=k3x+b3,由题意,得![]()
解得:![]()
∴y甲2=-20x+40,![]()
解得:![]()
设乙前往A地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙1=k1x,由题意,得![]()
设乙返回B地距离B地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙2=k2x+b2,由题意,![]()
∴y=-30x+60.
当![]() 时
时
∴![]()
![]()
![]()
【解析】解:(1)由图像上y轴的甲初始值得30,可知A、B两地间的距离为30千米
(1)由函数图象可以求出甲行驶的时间,就可以由路程÷时间求出甲行驶的速度;
(2)由相遇问题即为两直线相交问题;
(3)设甲在修车前y与x之间的函数关系式为y甲1=kx+b,甲在修车后y与x之间的函数关系式为y甲2=k3x+b3,乙前往A地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙1=k1x,设乙返回B地距离B地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙2=k2x+b2,由待定系数法求出解析式建立不等式组求出其解即可解得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=x+2交y轴于点A1 , 在x轴正方向上取点B1 , 使OB1=0A1;过点B1作A2B1⊥x轴,交l于点A2 , 在x轴正方向上取点B2 , 使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3 , 在x轴正方向上取点B3 , 使B2B3=B2A3记△OA1B1面积为S1,△B1A2B2面积为S2 , △B2A3B3面积为S3 , …则S2018等于.

-
科目: 来源: 题型:
查看答案和解析>>【题目】能把一个任意三角形分成面积相等的两部分是( )
A. 角平分线 B. 中线 C. 高 D. A、B、C都可以
-
科目: 来源: 题型:
查看答案和解析>>【题目】-64的立方根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一等腰三角形两边长分别为3,4.则这个等腰三角形的周长为( )
A. 7 B. 11 C. 7或10 D. 10或11
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知9的算术平方根为a,b的绝对值为4,求a-b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:能够成为直角三角形三条边长的三个正整数
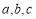 ,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: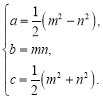 其中
其中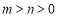 ,
, 是互质的奇数.
是互质的奇数.应用,当
 时,求有一边长为5的直角三角形的另外两条边长.
时,求有一边长为5的直角三角形的另外两条边长.
相关试题

