【题目】下列计算正确的是( )
A.20170=0
B.![]() =±9
=±9
C.(x2)3=x5
D.3﹣1= ![]()
参考答案:
【答案】D
【解析】解:A、非零的零次幂等于1,故A不符合题意;
B、81的算术平方根是9,故B不符合题意;
C、幂的乘方底数不变指数相乘,故C不符合题意;
D、负整数指数幂与正整数指数幂互为倒数,故D符合题意;
故选:D.
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本,需要知道零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到一个问题:在
 中,
中, ,
,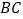 ,
, 三边的长分别为
三边的长分别为 、
、 、
、 ,求
,求 的面积.
的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为
 ),再在网格中画出格点
),再在网格中画出格点 (即
(即 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.参考小明解决问题的方法,完成下列问题:
(
 )图
)图 是一个
是一个 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为 ) .
) .①利用构图法在答卷的图
 中画出三边长分别为
中画出三边长分别为 、
、 、
、 的格点
的格点 .
. ②计算①中
 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)(
 )如图
)如图 ,已知
,已知 ,以
,以 ,
, 为边向外作正方形
为边向外作正方形 ,
, ,连接
,连接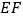 .
.①判断
 与
与 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.②若
 ,
, ,
, ,直接写出六边形
,直接写出六边形 的面积为__________.
的面积为__________.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国几家银行的标志,其中即是轴对称图形又是中心对称图形的有( )

A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=
 (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).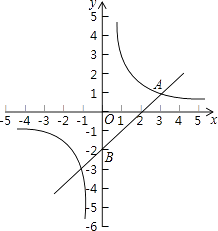
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x>0,现规定符号[x]表示大于或等于x的最小整数,如[0.5]=1,[4.3]=5,[6]=6……
(1)填空:[
 ]=_____,[8.05]=______;若[x]=5,则x的取值范围是________.
]=_____,[8.05]=______;若[x]=5,则x的取值范围是________.(2)某市的出租车收费标准如下:3 km以内(包括3km)收费5元,超过3 km的,每超过1km,加收1.2元(不足1 km按1 km计算).设所行驶的路程为x(km),用含[x]的式子表示出当x>3时的乘车费用.
(3) 在(2)的条件下,某乘客乘出租车后付费18.2元,求该乘客所乘路程的取值范围.
-
科目: 来源: 题型:
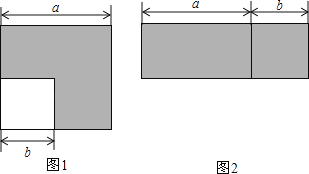
查看答案和解析>>【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
相关试题

