搜索
【题目】因式分解：
（1）m2（n﹣2）﹣m（2﹣n）
（2）4（a﹣b）2+1+4（a﹣b）
参考答案：
【答案】（1）m（n﹣2）（m+1）；（2）（2a﹣2b+1）2
【解析】试题分析：（1）提取公式因m（n﹣2）；（2）运用完全平方公式因式分解.
试题解析：
（1）m2（n﹣2）﹣m（2﹣n）=m（n﹣2）（m+1）；
（2）4（a﹣b）2+1+4（a﹣b）=[2（a﹣b）+1]2=（2a﹣2b+1）2 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若线段a，b，c，d成比例，其中a=3cm，b=6cm，c=2cm，则d=________．
-
科目： 来源： 题型：
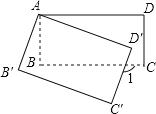
查看答案和解析>>【题目】如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我省旅游胜地三清山二月份某天最高气温是11℃，最低气温是-2℃，那么这天的温差（最高气温与最低气温的差）是________℃.
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的二次三项式4x+mx+1是完全平方式，则m=________
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（﹣3，0）、（0，4），抛物线y=
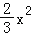+bx+c经过B点，且顶点在直线x=
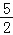上．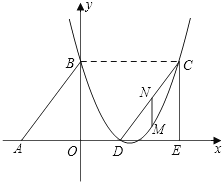
（1）求抛物线对应的函数关系式；
（2）若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；
（3）在（2）的前提下，若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为l．求l与t之间的函数关系式，并求l取最大值时，点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请写出一个负无理数____________．
相关试题
