【题目】如图,已知经过点D(2,﹣![]() )的抛物线y=
)的抛物线y=![]() (x+1)(x﹣3)(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.
(x+1)(x﹣3)(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.
(1)填空:m的值为 , 点A的坐标为;
(2)根据下列描述,用尺规完成作图(保留作图痕迹,不写作法):连接AD,在x轴上方作射线AE,使∠BAE=∠BAD,过点D作x轴的垂线交射线AE于点E;
(3)动点M、N分别在射线AB、AE上,求ME+MN的最小值;
参考答案:
【答案】
(1)
解: ∵抛物线y=![]() (x+1)(x﹣3)经过点D(2,﹣
(x+1)(x﹣3)经过点D(2,﹣![]() ),
),
∴m=![]() ,
,
把m=![]() 代入y=
代入y=![]() (x+1)(x﹣3),得y=
(x+1)(x﹣3),得y=![]() (x+1)(x﹣3),
(x+1)(x﹣3),
即y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ;
;
令y=0,得(x+1)(x﹣3)=0,
解得x=﹣1或3,
∴A(﹣1,0),B(3,0);
(2)
解: 如图1所示;

(3)
解: 过点D作射线AE的垂线,垂足为N,交AB于点M,设DE与x轴交于点H,如图2,

由(1)(2)得点D与点E关于x轴对称,
∴MD=ME,
∵AH=3,DH=![]() ,
,
∴AD=2![]() ,
,
∴∠BAD=∠BAE=30°,
∴∠DAN=60°,
∴sin∠DAN=![]() ,
,
∴sin60°=![]() ,
,
∴DN=3,
∵此时DN的长度即为ME+MN的最小值,
∴ME+MN的最小值为3;
【解析】(1)把点D坐标代入抛物线y=![]() (x+1)(x﹣3),即可得出m的值,再令y=0,即可得出点A,B坐标;
(x+1)(x﹣3),即可得出m的值,再令y=0,即可得出点A,B坐标;
(2)根据尺规作图的要求,画出图形,如图1所示;
(3)过点D作射线AE的垂线,垂足为N,交AB于点M,此时DN的长度即为ME+MN的最小值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=
 (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①S△ADB=S△ADC;
②当0<x<3时,y1<y2;
③如图,当x=3时,EF= ;
;
④当x>0时,y1随x的增大而增大,y2随x的增大而减小.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果精确到0.1米,参考数据:
 =1.41,
=1.41, =1.73).
=1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB=90°,AO=
 ,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F.点P从点A出发沿射线AO以每秒
,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F.点P从点A出发沿射线AO以每秒 个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动.设运动的时间为t秒.
个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动.设运动的时间为t秒.
(1)当t= 时,PQ∥EF;
(2)若P、Q关于点O的对称点分别为P′、Q′,当线段P′Q′与线段EF有公共点时,t的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.
[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.
根据“边角边”,可证△CEH≌ , 得EH=ED.
在Rt△HBE中,由定理,可得BH2+EB2=EH2 , 由BH=AD,可得AD、DE、EB之间的等量关系是 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2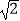 ,运用小聪同学探究的结论,求正方形的边长及MN的长.
,运用小聪同学探究的结论,求正方形的边长及MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.

(1)根据图象求出b关于a的函数解析式(包括自变量的取值范围);
(2)若农场到B公司的路程是农场到A公司路程的2倍,农场到A公司的路程为m千米,设农场从A公司购买x吨铵肥,购买8吨铵肥的总费用为y元(总费用=购买铵肥费用+运输费用),求出y关于x的函数解析式(m为常数),并向农场建议总费用最低的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015朝阳)如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
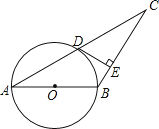
(1)判断DE与⊙O的位置关系并说明理由;
(2)若AC=16,tanA= , 求⊙O的半径.
, 求⊙O的半径.
相关试题

