【题目】如图,一场篮球赛中,球员甲跳起投篮,已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,当球水平运行4 m时达到离地面的最大高度4 m.设篮球运行的轨迹为抛物线的一部分,篮圈距地面3 m,在篮球比赛中,当进攻方球员要投篮时,防守方球员常借身高优势及较强的弹跳封杀对方,这就是平常说的盖帽.(注:盖帽应在球达到最高点前进行,否则就是“干扰球”,属犯规.)
m,与篮圈中心的水平距离为7 m,当球水平运行4 m时达到离地面的最大高度4 m.设篮球运行的轨迹为抛物线的一部分,篮圈距地面3 m,在篮球比赛中,当进攻方球员要投篮时,防守方球员常借身高优势及较强的弹跳封杀对方,这就是平常说的盖帽.(注:盖帽应在球达到最高点前进行,否则就是“干扰球”,属犯规.)
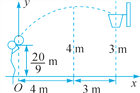
(1)问:此球能否投中?
(2)此时,防守方球员乙前来盖帽,已知乙的最大摸球高度为3.19 m,则他如何做才能成功?
参考答案:
【答案】(1) 能投中;(2) 防守方球员乙应在球员甲身前,且距离甲1.3 m以内盖帽才能成功.
【解析】试题分析:①先求出篮球运动抛物线的解析式,把坐标(7,3)代入判断是否满足,则即可确定篮球是否能准确投中;
②将由y=3.19代入函数的解析式求得x值,进而得出答案.
试题解析:
(1)以篮球所在竖直方向的直线与地面的交点O为原点,脚与篮圈底所在直线为x轴,篮球所在竖直方向的直线为y轴建立直角坐标系.由题意可知抛物线经过点![]() ,顶点是(4,4),篮圈中心的坐标是(7,3),∴可设抛物线的函数表达式为y=a(x-4)2+4(a≠0).
,顶点是(4,4),篮圈中心的坐标是(7,3),∴可设抛物线的函数表达式为y=a(x-4)2+4(a≠0).
把点![]() 的坐标代入函数表达式,
的坐标代入函数表达式,
得a(0-4)2+4=![]() ,∴a=-
,∴a=-![]() .
.
∴篮球运行的抛物线的函数表达式为y=-![]() (x-4)2+4.
(x-4)2+4.
当x=7时,y=-![]() ×(7-4)2+4=3,
×(7-4)2+4=3,
即抛物线过篮圈中心,∴此球能投中.
(2)当y=3.19时,-![]() (x-4)2+4=3.19,
(x-4)2+4=3.19,
解得x1=1.3,x2=6.7.
∵盖帽应在球达到最高点前进行(即x<4),
∴x=1.3.
∴防守方球员乙应在球员甲身前,且距离甲1.3 m以内盖帽才能成功.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一组数据:3,5,5,6,7,这组数据的众数为( )
A.3
B.5
C.6
D.7 -
科目: 来源: 题型:
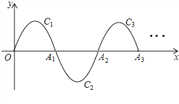
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是关于x的一元二次方程x2+kx+4=0的一个根,则k的值为( )
A.5B.﹣5C.3D.﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )

A.y=2x+3
B.y=x﹣3
C.y=2x﹣3
D.y=﹣x+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,不确定事件是( )
A.在空气中,汽油遇上火就燃烧
B.向上用力抛石头,石头落地
C.任何数和零相乘,积仍为零
D.明天是雨天 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组线段中,可以构成直角三角形的是( )
A. 4,5,6B. 6,8,10C. 2,3,4D. 1,1,2
相关试题

