【题目】)如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE。

(1)试说明△BDE≌△CDF
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
参考答案:
【答案】(1)理由见解析;(2)四边形BECF是平行四边形.理由见解析.
【解析】
试题分析:(1)利用CF∥BE和D是BC边的中点可以得到全等条件证明△BDE≌△CDF;
(2)根据(1)的结论和平行四边形的判定容易证明四边形BECF是平行四边形.
试题解析:(1)∵CF∥BE,
∴∠FCD=∠EBD.
∵D是BC的中点,
∴CD=BD.
∵∠FDC=∠EDB,
∴△CDF≌△BDE(ASA).
(2)四边形BECF是平行四边形.
理由:∵△CDF≌△BDE,
∴DF=DE,DC=DB.
∴四边形BECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初中生的视力状况受到全社会的广泛关注,某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,如图是利用所得数据绘制的频数分布直方图(长方形的高表
示该组人数),根据图中所提供的信息,回答下列问题:

(1)本次调查共抽测了 名学生,占该市初中生总数的百分比是 ;
(2)从左到右五个小组的频率之比是 ;
(3)如果视力在4.9~5.1(含4.9,5.1)均属正常,则全市有 名初中生的视力正常, 视力正常的合格率是 .
(4)此统计图说明了什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中为无理数的是( )
A.﹣1 B.3.14 C.π D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,0,1,2这四个数中,既不是正数也不是负数的是( ).
A.﹣1 B.0 C.1 D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,正中设计一个圆形喷水池,若四周圆形和中间圆形的半径均为
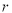 米,广场长为
米,广场长为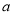 米,宽为
米,宽为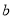 米.
米.(1)请列式表示广场空地的面积;
(2)若休闲广场的长为500米,宽为300米,圆形花坛的半径为20米,求广场空地的面积(计算结果保留
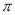 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】【知识背景】在学习计算框图时,可以用“
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条)
【尝试解决】
(1)①如图1,当输入数x=﹣2时,输出数y=__________;
②如图2,第一个“
 ”内,应填__________; 第二个“
”内,应填__________; 第二个“ ”内,应填__________;
”内,应填__________;(2)①如图3,当输入数x=﹣1时,输出数y=__________;②如图4,当输出的值y=17,则输入的值x=__________;
【实际应用】
(3)为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量x,输出数为水费y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】去括号正确的是( )
A. -(a+b-c)=-a+b-c
B. -2(a+b-3c)=-2a-2b+6c
C. -(-a-b-c)=-a+b+c
D. -(a-b-c)=-a+b-c
相关试题

