【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣![]() x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒![]() 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?

参考答案:
【答案】(1) y=﹣![]() x2﹣2
x2﹣2![]() x+3
x+3![]() ;(2) P的坐标为(﹣4,﹣
;(2) P的坐标为(﹣4,﹣![]() )和(﹣6,﹣
)和(﹣6,﹣![]() );(3) (1,﹣4
);(3) (1,﹣4![]() ).
).
【解析】
试题分析:(1)根据二次函数的交点式确定点A、B的坐标,求出直线的解析式,求出点D的坐标,求出抛物线的解析式;(2)作PH⊥x轴于H,设点P的坐标为(m,n),分△BPA∽△ABC和△PBA∽△ABC,根据相似三角形的性质计算即可;(3)作DM∥x轴交抛物线于M,作DN⊥x轴于N,作EF⊥DM于F,根据正切的定义求出Q的运动时间t=BE+EF时,t最小即可.
试题解析:(1)∵y=a(x+3)(x﹣1),
∴点A的坐标为(﹣3,0)、点B两的坐标为(1,0),
∵直线y=﹣![]() x+b经过点A,
x+b经过点A,
∴b=﹣3![]() ,
,
∴y=﹣![]() x﹣3
x﹣3![]() ,
,
当x=2时,y=﹣5![]() ,
,
则点D的坐标为(2,﹣5![]() ),
),
∵点D在抛物线上,
∴a(2+3)(2﹣1)=﹣5![]() ,
,
解得,a=﹣![]() ,
,
则抛物线的解析式为y=﹣![]() (x+3)(x﹣1)=﹣
(x+3)(x﹣1)=﹣![]() x2﹣2
x2﹣2![]() x+3
x+3![]() ;
;
(2)作PH⊥x轴于H,
设点P的坐标为(m,n),
当△BPA∽△ABC时,∠BAC=∠PBA,
∴tan∠BAC=tan∠PBA,即![]() =
=![]() ,
,
∴![]() =
=![]() ,即n=﹣a(m﹣1),
,即n=﹣a(m﹣1),
∴![]() ,
,
解得,m1=﹣4,m2=1(不合题意,舍去),
当m=﹣4时,n=5a,
∵△BPA∽△ABC,
∴![]() =
=![]() ,即AB2=ACPB,
,即AB2=ACPB,
∴42=![]()
![]() ,
,
解得,a1=![]() (不合题意,舍去),a2=﹣
(不合题意,舍去),a2=﹣![]() ,
,
则n=5a=﹣![]() ,
,
∴点P的坐标为(﹣4,﹣![]() );
);
当△PBA∽△ABC时,∠CBA=∠PBA,
∴tan∠CBA=tan∠PBA,即![]() =
=![]() ,
,
∴![]() =
=![]() ,即n=﹣3a(m﹣1),
,即n=﹣3a(m﹣1),
∴![]() ,
,
解得,m1=﹣6,m2=1(不合题意,舍去),
当m=﹣6时,n=21a,
∵△PBA∽△ABC,
∴![]() =
=![]() ,即AB2=BCPB,
,即AB2=BCPB,
∴42=![]()
![]() ,
,
解得,a1=![]() (不合题意,舍去),a2=﹣
(不合题意,舍去),a2=﹣![]() ,
,
则点P的坐标为(﹣6,﹣![]() ),
),
综上所述,符合条件的点P的坐标为(﹣4,﹣![]() )和(﹣6,﹣
)和(﹣6,﹣![]() );
);
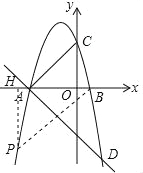
(3)作DM∥x轴交抛物线于M,作DN⊥x轴于N,作EF⊥DM于F,
则tan∠DAN=![]() =
=![]() =
=![]() ,
,
∴∠DAN=60°,
∴∠EDF=60°,
∴DE=![]() =
=![]() EF,
EF,
∴Q的运动时间t=![]() +
+![]() =BE+EF,
=BE+EF,
∴当BE和EF共线时,t最小,
则BE⊥DM,E(1,﹣4![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A:绿化造林. B:汽车限行.C:拆除燃煤小锅炉.D:使用清洁能源.调查过程中随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:

(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整;
(3)求图2中D项目对应的扇形的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2016年到2018年,该中学三年为新增电脑共投资多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面文字,根据所给信息解答下面问题:把几个数用大括号括起来,中间用逗号隔开,如:{3,4};{﹣3,6,8,18},其中大括号内的数称其为集合的元素.如果一个集合满足:只要其中有一个元素a,使得﹣2a+4也是这个集合的元素,这样的集合称为条件集合.例如;{3,﹣2},因为﹣2×3+4=﹣2,﹣2恰好是这个集合的元素所以吕{3,﹣2}是条件集合:例如;(﹣2,9,8,},因为﹣2×(﹣2)+4=8,8恰好是这个集合的元素,所以{﹣2,9,8,}是条件集合.
(1)集合{﹣4,12}是否是条件集合?
(2)集合{
 ,﹣
,﹣ ,
, }是否是条件集合?
}是否是条件集合?(3)若集合{8,n}和{m}都是条件集合.求m、n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线 A1C和OB1交于点M1;以M1A1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;……依此类推,这样作的第n 个正方形对角线交点Mn的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】李师傅一家开车去旅游,出发前查看了油箱里有50升油,出发后先后走了城市路、高速路、山路最终到达旅游地点,下面的两幅图分别描述了行驶里程及耗油情况,下面的描述错误的是( )
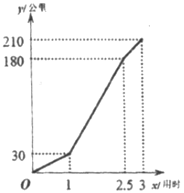
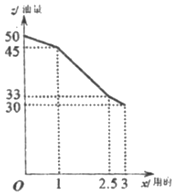
A. 此车一共行驶了210公里
B. 此车高速路一共用了12升油
C. 此车在城市路和山路的平均速度相同
D. 以此车在这三个路段的综合油耗判断50升油可以行驶约525公里
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
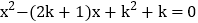 。
。(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
相关试题

