【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛.从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计频数分布直方图(未完成)和扇形图如下,请解答下列问题: 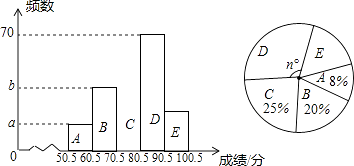
(1)A组的频数a比B组的频数b小24,样本容量 , a为:
(2)n为°,E组所占比例为%:
(3)补全频数分布直方图;
(4)若成绩在80分以上优秀,全校共有2000名学生,估计成绩优秀学生有名.
参考答案:
【答案】
(1)200;16
(2)126;12
(3)解:C组的频数为200×25%=50,E组的频数为200﹣16﹣40﹣50﹣70=24,
补全频数分布直方图为:
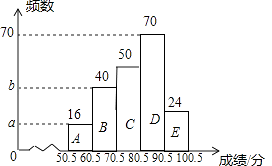
(4)940
【解析】解:(1.)调查的总人数为24÷(20%﹣8%)=200, 所以a=200×8%=16,b=200×20%=40,
所以答案是:200,16;
(2.)D部分所对的圆心角=360°× ![]() =126°,即n=126,
=126°,即n=126,
E组所占比例为1﹣(8%+20%+25%+ ![]() ×100%)=12%,
×100%)=12%,
所以答案是126,12;
(4.)2000× ![]() =940,
=940,
所以估计成绩优秀的学生有940人.
【考点精析】掌握总体、个体、样本、样本容量和频数分布直方图是解答本题的根本,需要知道所要考察的全体对象叫总体,组成总体的每一个考察对象叫个体,被抽取的那部分个体组成总体的一个样本,样本中个体的数目叫这个样本的容量(样本容量没有单位);特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,且BF=AC。求证:ED平分∠FEC。

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(xy3)2的结果是( )
A. xy6 B. x2y3 C. x2y6 D. x2y5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
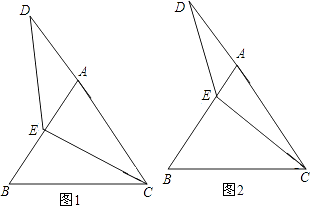
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(0,0),B(2,﹣2),C(4,0),D(2,2),则以这四个点为顶点的四边形ABCD是( )
A. 正方形 B. 菱形 C. 梯形 D. 矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2a2)3的结果是( )
A. 2a5 B. 2a6 C. 6a6 D. 8a6
相关试题

