【题目】(14分)如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?

参考答案:
【答案】(1)(1,4);y=﹣(x﹣1)2+4;
(2)当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;
时,△PCQ为直角三角形;
(3)当t=2时,△ACQ的面积最大,最大值是1.
【解析】(1)由抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,可求得点A的坐标,然后设抛物线的解析式为y=a(x﹣1)2+4,将点C代入即可求得答案;
(2)分别从∠QPC=90°与∠PQC=90°,利用cos∠QPC求解即可求得答案;
(3)首先设直线AC的解析式为y=kx+b,利用待定系数法即可求得直线AC的解析式,然后求得点Q的坐标,继而求得S△ACQ=S△AFQ+S△CPQ=![]() FQAG+
FQAG+![]() FQDG=
FQDG=![]() FQ(AG+DG)=
FQ(AG+DG)=![]() (t﹣2)2+1,则可求得答案.
(t﹣2)2+1,则可求得答案.
解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,
∴点A坐标为(1,4),
设抛物线的解析式为y=a(x﹣1)2+4,
把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,
解得a=﹣1.
∴抛物线的解析式为:y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)依题意有:OC=3,OE=4,
∴CE=![]() =5,
=5,
当∠QPC=90°时,
∵cos∠QPC=![]() ,
,
∴![]() ,
,
解得t=![]() ;
;
当∠PQC=90°时,
∵cos∠QCP=![]() ,
,
∴![]() ,
,
解得t=![]() .
.
∴当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;
时,△PCQ为直角三角形;
(3)∵A(1,4),C(3,0),
设直线AC的解析式为y=kx+b,则![]() ,解得:
,解得: ![]() .
.
故直线AC的解析式为y=﹣2x+6.
∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+![]() ,
,
∴Q点的横坐标为1+![]() ,
,
将x=1+![]() 代入y=﹣(x﹣1)2+4中,得y=4﹣
代入y=﹣(x﹣1)2+4中,得y=4﹣![]() .
.
∴QF=(4﹣![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣![]() ,
,
∴S△ACQ=S△AFQ+S△CPQ=![]() FQAG+
FQAG+![]() FQDG=
FQDG=![]() FQ(AG+DG)=
FQ(AG+DG)=![]() FQAD=
FQAD=![]() ×2(t﹣
×2(t﹣![]() )=﹣
)=﹣![]() (t﹣2)2+1,
(t﹣2)2+1,
∴当t=2时,△ACQ的面积最大,最大值是1.
“点睛”考查了二次函数综合题,涉及的知识点有:抛物线的对称轴,矩形的性质,待定系数法求抛物线的解析式,待定系数法求直线的解析式,勾股定理,三角形面积,二次函数的最值,以及分类思想的运用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 、
、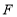 在直线
在直线 上,点
上,点 在线段
在线段 上,
上, 与
与 交于点
交于点 ,
, .求证:
.求证: .(完成以下填空)
.(完成以下填空)证明:∵
 (已知),
(已知),且
 ( )
( )∴
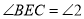 (等量代换)
(等量代换)∴
 ( )
( )∴
 ( )
( )又∵
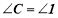 (已知)
(已知)∴
 (等量代换)
(等量代换)∴
 ( )
( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△
 A1B1C;
A1B1C;

(2)以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2,并写出点
 的坐标________________.
的坐标________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电器城经销A型号彩电,今年四月份每台彩电售价为2000元,与去年同期相比,结果卖出彩电的数量相同,但去年销售额为5万元,今年销售额只有4万元.
(1)问去年四月份每台A型号彩电售价是多少元?
(2)为了改善经营,电器城决定再经销B型号彩电.已知A型号彩电每台进货价为1800元,B型号彩电每台进货价为1500元,电器城预计用不多于
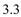 万元且不少于
万元且不少于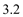 万元的资金购进这两种彩电共20台,问有哪几种进货方案?
万元的资金购进这两种彩电共20台,问有哪几种进货方案?(3)电器城准备把A型号彩电继续以原价每台2000元的价格出售,B型号彩电以每台1800元的价格出售,在这批彩电全部卖出的前提下,如何进货才能使电器城获利最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某集团决定购买
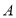 、
、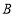 两种型号的污水处理设备共10台,其中每台价格及月处理污水量如下表:
两种型号的污水处理设备共10台,其中每台价格及月处理污水量如下表: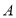
价格(万元/元)
15
12
处理污水量(吨/月)
250
220
经预算,该集团准备购买设备的资金不高于130万元.
(1)请你设计该企业有哪几种购买方案?
(2)试通过计算,说明哪种方案处理污水多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )

A. ②③④ B. ①②③ C. ②③ D. ①④
-
科目: 来源: 题型:
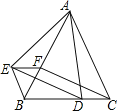
查看答案和解析>>【题目】如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
相关试题

