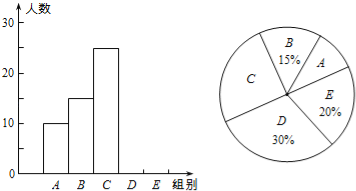
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
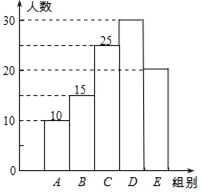
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
参考答案:
【答案】(1)30,20;(2)90°;(3)450.
【解析】试题分析:(1)根据条形图和扇形图确定B组的人数环绕所占的百分比求出样本容量,求出m、n的值;
(2)求出C组”所占的百分比,得到所对应的圆心角的度数;
(3)求出不合格人数所占的百分比,求出该校本次听写比赛不合格的学生人数.
试题解析:(1)从条形图可知,B组有15人,
从扇形图可知,B组所占的百分比是15%,D组所占的百分比是30%,E组所占的百分比是20%,
15÷15%=100,
100×30%=30,
100×20%=20,
∴m=30,n=20.
故答案为:30;20;
统计图如下:
(2)“C组”所对应的圆心角的度数是25÷100×360°=90°.
故答案为:90°;
(3)估计这所学校本次听写比赛不合格的学生人数为:900×(10%+15%+25%)=450人.
-
科目: 来源: 题型:
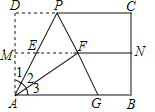
查看答案和解析>>【题目】如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.求证:
(1)△AFG≌△AFP;
(2)△APG为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=
 x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x=  上.
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其中部分图象如图所示,下列结论错误的是( )
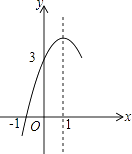
A.4ac<b2
B.方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
C.当y>0时,x的取值范围是﹣1≤x<3
D.当x<0时,y随x增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.
B.
C.
D.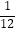
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
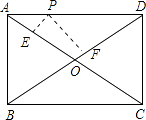
A.4.8
B.5
C.6
D.7.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的对角线AC,BD交于点O,点E,F分别是OB,OC上的动点.当动点E,F满足BE=CF时.
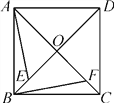
(1)写出所有以点E或F为顶点的全等三角形;(不得添加辅助线)
(2)求证:AE⊥BF.
相关试题

