【题目】下列说法正确的是( )
A. 若AC=BC,则点C是线段AB的中点
B. 若∠AOC=∠BOC,则直线OC是∠AOB的平分线
C. 连接A、B的线段叫做A、B两点间的距离
D. 若DE=5,DF=8,EF=13,则点D在线段EF上
参考答案:
【答案】D
【解析】
根据线段中点、角平分线、两点之间距离意义可判断A、B、C选项正误;D选项根据有公共端点的两线段和是否等于最长一条来判断是否共线.
解:A:点C不一定在线段AB上,故错误;
B:角平分线是射线,且射线OC不一定在∠AOB内部,故错误;
C:连接A、B的线段的长度是A、B两点间的距离,故错误;
D:因为DE+DF=EF故点D在线段EF上,故正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前,组委会拟定了四种记分方案:方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:评委编号
1
2
3
4
5
6
7
8
9
10
打分
7.0
7.8
3.2
8.0
8.4
8.4
9.8
8.0
8.4
8.0
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
-
科目: 来源: 题型:
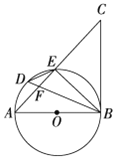
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D是弧AE上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF·DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
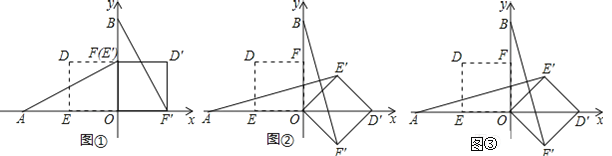
(1)如图②,当α=135°时,求AE′,BF′的长;
(2)如图③,当0°﹤α﹤180°时, AE′和BF′有什么位置关系;
(3)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.

相关试题

