【题目】如图,直线EF分别与直线AB,CD相交于点G、H,已知∠1=∠2=50°,GM平分∠HGB交直线CD于点M.则∠3=( ) 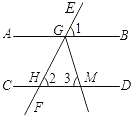
A.60°
B.65°
C.70°
D.130°
参考答案:
【答案】B
【解析】解:∵∠1=50°, ∴∠BGH=180°﹣50°=130°,
∵GM平分∠HGB,
∴∠BGM=65°,
∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
∴∠3=∠BGM=65°(两直线平行,内错角相等).
故选B.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度由-4℃上升7℃后是____________ ℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2 , 直线l3和直线l1 , l2交于点C和D,直线l3上有一点P.
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;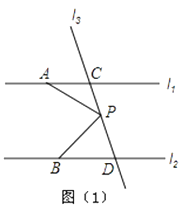
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试写出∠PAC,∠APB,∠PBD之间的关系,并说明理由.(图3只写结论,不写理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是_____________.
-
科目: 来源: 题型:
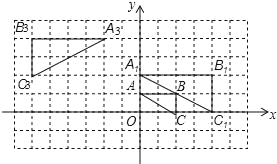
查看答案和解析>>【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.
(1)△ABC与△A1B1C1的位似比等于 ;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正多边形的内角和是外角和的3倍,那么这个正多边形的边数为( )
A.5B.6C.7D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区在规划设计时,准备在两幢楼房之间,设置一块周长为120米的长方形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,下面列出的方程正确的是( )
A.2(x﹣10)=120
B.2[x+(x﹣10)]=120
C.2(x+10)=120
D.2[x+(x+10)]=120
相关试题

