搜索
【题目】以坐标原点O为圆心，作半径为2的圆，若直线y=﹣x+b与⊙O相交，则b的取值范围是（ ）
A.0≤b＜2 
B.﹣2 
C.﹣2 
2 
D.﹣2 ＜b＜2
参考答案：
【答案】D
【解析】解：当直线y=﹣x+b与圆相切，且函数经过一、二、四象限时，如图．
在y=﹣x+b中，令x=0时，y=b，则与y轴的交点是（0，b），
当y=0时，x=b，则A的交点是（b，0），
则OA=OB，即△OAB是等腰直角三角形．
连接圆心O和切点C．则OC=2．
则OB= 
OC=2 ．即b=2 ；
同理，当直线y=﹣x+b与圆相切，且函数经过二、三、四象限时，b=﹣2 ．
则若直线y=﹣x+b与⊙O相交，则b的取值范围是﹣2 ＜b＜2 ．
求出直线y=﹣x+b与圆相切，且函数经过一、二、四象限，和当直线y=﹣x+b与圆相切，且函数经过二、三、四象限时b的值，则相交时b的值在相切时的两个b的值之间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解答题
（1）如图1，在正方形ABCD中，点E，F分别在BC，CD上，AE⊥BF于点M，求证：AE=BF；
（2）如图2，将 （1）中的正方形ABCD改为矩形ABCD，AB=2，BC=3，AE⊥BF于点M，探究AE与BF的数量关系，并证明你的结论．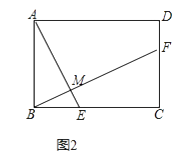
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线l的解析式为y=﹣2x+2，分别交x轴、y轴于点A，B．
（1）写出A，B两点的坐标，并画出直线l的图象；
（2）将直线l向上平移4个单位得到l1 ， l1交x轴于点C． ①作出l1的图象，
②l1的解析式是 ．
（3）将直线l绕点A顺时针旋转90°得到l2 ， l2交l1于点D． ①作出l2的图象，
②tan∠CAD= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在距离铁轨200米的B处，观察由南宁开往百色的“和谐号”动车，当动车车头在A处时，恰好位于B处的北偏东60°方向上；10秒钟后，动车车头到达C处，恰好位于B处的西北方向上，则这时段动车的平均速度是（ ）米/秒．
A.20（
+1）
B.20（ ﹣1）
C.200
D.300 -
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的不等式组
的解集中至少有5个整数解，则正数a的最小值是（ ）
A.3
B.2
C.1
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：用“十字相乘法”分解因式2x2﹣x﹣3的方法．
（i）二次项系数2=1×2；
（ii）常数项﹣3=﹣1×3=1×（﹣3），验算：“交叉相乘之和”；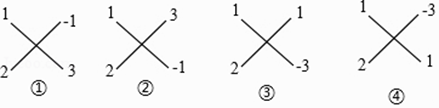
1×3+2×（﹣1）=1 1×（﹣1）+2×3=5 1×（﹣3）+2×1=﹣1 1×1+2×（﹣3）=﹣5
（iii）发现第③个“交叉相乘之和”的结果1×（﹣3）+2×1=﹣1，等于一次项系数﹣1．
即：（x+1）（2x﹣3）=2x2﹣3x+2x﹣3=2x2﹣x﹣3，则2x2﹣x﹣3=（x+1）（2x﹣3）．
像这样，通过十字交叉线帮助，把二次三项式分解因式的方法，叫做十字相乘法．仿照以上方法，分解因式：3x2+5x﹣12= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众，有一期甲、乙两人被抽为场外幸运观众，他们获得了一次抽奖的机会，在如图所示的翻奖牌的正面4个数字中任选一个，选中后翻开，可以得到该数字反面的奖品，第一个人选中的数字第二个人不能再选择了．
（1）如果甲先抽奖，那么甲获得“手机”的概率是多少？
（2）小亮同学说：甲先抽奖，乙后抽奖，甲、乙两人获得“手机”的概率不同，且甲获得“手机”的概率更大些．你同意小亮同学的说法吗？为什么？请用列表或画树状图分析．
相关试题
