【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.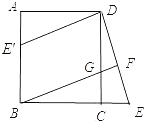
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
参考答案:
【答案】
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
又∵CG=CE,
∴△BCG≌△DCE.
(2)解:四边形E′BGD是平行四边形.理由如下:
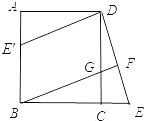
∵△DCE绕D顺时针旋转90°得到△DAE′,
∴CE=AE′.
∵CE=CG,
∴CG=AE′.
∵四边形ABCD是正方形,
∴BE′∥DG,AB=CD.
∴AB﹣AE′=CD﹣CG.
即BE′=DG.
∴四边形E′BGD是平行四边形.
【解析】(1)首先依据正方形的性质得到:BC=CD,∠BCD=∠DCE=90°,然后再依据SAS可证明△BCG≌△DCE;
(2)由(1)得BG=DE,又由旋转的性质知AE′=CE=CG,然后依据等式的性质可证明BE′=DG,最后依据一组对边平行且相等的四边形是平行四边形可证明四边形E′BGD为平行四边形.
【考点精析】本题主要考查了平行四边形的判定和正方形的性质的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组数为边长,不能组成直角三角形的是( )
A. 3、4、5 B. 7、24、25 C. 6、8、10 D. 3、5、7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=﹣2x+3与y=﹣
 x+m的图象交于P(n,﹣2).
x+m的图象交于P(n,﹣2).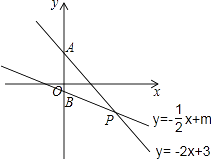
(1)求出m、n的值;
(2)求出△ABP的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值.(2x+3)(2x﹣3)﹣4x(x﹣1)+(x﹣2)2 , 其中x=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年政府工作报告中指出,5年来我国有约80000000农业转移人口成为城镇居民.用科学记数法表示数据80000000,其结果是( )
A.80×106B.0.8×108C.8×107D.8×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
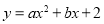 过B(﹣2,6),C(2,2)两点.
过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线
 向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市经销A、B两种商品,A种商品每件进价20元,售价30元;B种商品每件进价35元,售价48元.
(1)该超市准备用800元去购进A、B两种商品若干件,怎样购进才能使超市经销这两种商品所获利润最大?(其中B种商品不少于7件)
(2)在“五一”期间,该商场对A、B两种商品进行如下优惠促销活动:打折前一次购物总金额
优惠措施
不超过300元
不优惠
超过300元且不超过400元
售价打八折
超过400元
售价打七折
促销活动期间小颖去该超市购买A种商品,小华去该超市购买B种商品,分别付款210元与268.8元.促销活动期间小明决定一次去购买小颖和小华购买的同样多的商品,他需付款多少元?
相关试题

