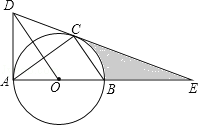
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
参考答案:
【答案】(1)、证明过程见解析;(2)、![]() .
.
【解析】
试题分析:(1)、连结OC,根据切线得出∠BAD=90°,然后得出△OCD和△OAD全等,从而得出∠OCD=∠OAD=90°,得出切线;(2)、设半径为r,则OE=AE﹣OA=6﹣r,OC=r,根据Rt△OCE的勾股定理求出r的值,然后根据△COE的面积减去扇形BOC的面积得出答案.
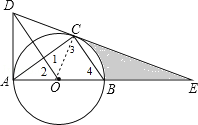
试题解析:(1)、连结OC,如图, ∵AD为⊙O的切线,∴AD⊥AB,∴∠BAD=90°,
∵OD∥BC,∴∠1=∠3,∠2=∠4, ∵OB=OC,∴∠3=∠4,∴∠1=∠2,
在△OCD和△OAD中,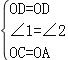 ,∴△AOD≌△COD(SAS); ∴∠OCD=∠OAD=90°,
,∴△AOD≌△COD(SAS); ∴∠OCD=∠OAD=90°,
∴OC⊥DE,∴DE是⊙O的切线;
(2)、设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中,∵OC2+CE2=OE2,
∴r2+(2![]() )2=(6﹣r)2,解得r=2,∵tan∠COE=
)2=(6﹣r)2,解得r=2,∵tan∠COE=![]() =
=![]() =
=![]() ,∴∠COE=60°,
,∴∠COE=60°,
∴S阴影部分=S△COE﹣S扇形BOC=![]() ×2×2
×2×2![]() ﹣
﹣![]() =2
=2![]() ﹣
﹣![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
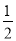
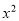 ﹣
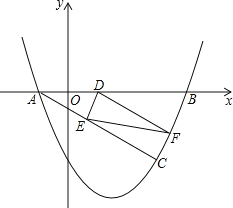
﹣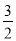 x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.(1)、求点A和点B的坐标;
(2)、求证:四边形DECF是矩形;
(3)、连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式加上3x2y﹣3xy2得x3﹣3x2y,则这个多项式是( )
A.x3+3xy2
B.x3﹣3xy2
C.x3﹣6x2y+3xy2
D.x3﹣6x2y﹣3x2y -
科目: 来源: 题型:
查看答案和解析>>【题目】大华服装厂生产一件秋冬季外套需面料1.2米,里料0.8米,已知面料的单价比里料的单价的2倍还多10元,一件外套的布料成本为76元.
(1)、求面料和里料的单价;
(2)、该款外套9月份投放市场的批发价为150元/件,出现购销两旺态势,10月份进入批发淡季,厂方决定采取打折促销.已知生产一件外套需人工等固定费用14元,为确保每件外套的利润不低于30元.设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
(3)、进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( )
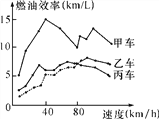
A. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
B. 以低于80 km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
C. 以高于80 km/h的速度行驶时,行驶相同路程,丙车比乙车省油
D. 以80 km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升
-
科目: 来源: 题型:
查看答案和解析>>【题目】设甲数为x,乙数比甲数的3倍少6,则乙数用代数式表示为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
相关试题

