【题目】如图所示,已知双曲线y=![]() (x<0)和y=
(x<0)和y=![]() (x>0),直线OA与双曲线y=
(x>0),直线OA与双曲线y=![]() 交于点A,将直线OA向下平移与双曲线y=
交于点A,将直线OA向下平移与双曲线y=![]() 交于点B,与y轴交于点P,与双曲线y=
交于点B,与y轴交于点P,与双曲线y=![]() 交于点C,S△ABC=6,
交于点C,S△ABC=6,![]() =
=![]() ,则k=( )
,则k=( )

A. ﹣6 B. ﹣4 C. 6 D. 4
参考答案:
【答案】D
【解析】
设A(xa,ya),B(xb,yb),C(xc,yc),则有xaya=xbyb=5,xcyc=k,由OA∥BC可得![]() ,过点A作AF⊥x轴于点F,BE⊥x轴于点E,CD⊥x轴于点D,由图可得:S△ABC=S梯形AFEB+S梯形BEDC﹣S梯形AFDC,代入坐标可得到:
,过点A作AF⊥x轴于点F,BE⊥x轴于点E,CD⊥x轴于点D,由图可得:S△ABC=S梯形AFEB+S梯形BEDC﹣S梯形AFDC,代入坐标可得到:![]() (ya+yb)(xb﹣xa)+
(ya+yb)(xb﹣xa)+![]() (yb+yc)(xc﹣xb)﹣
(yb+yc)(xc﹣xb)﹣![]() (ya+yc)(xc﹣xa)=6,整理得到:yaxb﹣xayb+ybxc﹣ycxb﹣yaxc+xayc=6,综上得到ybxc﹣ycxb=12,已知
(ya+yc)(xc﹣xa)=6,整理得到:yaxb﹣xayb+ybxc﹣ycxb﹣yaxc+xayc=6,综上得到ybxc﹣ycxb=12,已知![]() =
=![]() ,可得
,可得![]() =
=![]() ,yb=
,yb=![]() ,综合以上式子可得:10+
,综合以上式子可得:10+![]() xcyc=12,所以xcyc=4,即k=4.
xcyc=12,所以xcyc=4,即k=4.
设A(xa,ya),B(xb,yb),C(xc,yc),
则有xaya=xbyb=5,xcyc=k,
∵OA∥BC,
∴![]() ,
,
整理得到:yaxb﹣yaxc=xayb﹣xayc①,
过点A作AF⊥x轴于点F,BE⊥x轴于点E,CD⊥x轴于点D,
∵S△ABC=S梯形AFEB+S梯形BEDC﹣S梯形AFDC=6,
∴![]() (AF+BE)×EF+
(AF+BE)×EF+![]() (BE+CD)×DE﹣
(BE+CD)×DE﹣![]() (AF+CD)×DF=6,
(AF+CD)×DF=6,
代入坐标可得到:![]() (ya+yb)(xb﹣xa)+
(ya+yb)(xb﹣xa)+![]() (yb+yc)(xc﹣xb)﹣
(yb+yc)(xc﹣xb)﹣![]() (ya+yc)(xc﹣xa)=6,
(ya+yc)(xc﹣xa)=6,
整理得:yaxb﹣xayb+ybxc﹣ycxb﹣yaxc+xayc=6②,
①②联立得:ybxc﹣ycxb=12③,
由![]() =
=![]() ,可得:
,可得:![]() =
=![]() ,
,
即xb=![]() xc,
xc,
∴yb=![]() ,
,
代入③得:10+![]() xcyc=12,
xcyc=12,
解得:xcyc=4,
即k=4.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥BD,CD⊥BD

(1)若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;若不存在,请说明理由;
(2)若AB=9,CD=4,BD=12,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(3)若AB=9,CD=4,BD=15,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(4)若AB=m,CD=n,BD=l,请问m,n,l满足什么关系时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点?两个P点?三个P点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中有 A(-2,1), B(3, 1),C(2, 3)三点,请回答下列问题:

(1)在坐标系内描出点A, B, C的位置.
(2)画出
 关于直线x=-1对称的
关于直线x=-1对称的 ,并写出
,并写出 各点坐标.
各点坐标.(3)在y轴上是否存在点P,使以A,B, P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标:若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连OB,将纸片OABC沿OB折叠,使点A落在A′的位置,若OB=
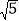 ,tan∠BOC=
,tan∠BOC= ,则点A′的坐标( )
,则点A′的坐标( )
A. (
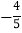 ,
,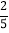 ) B. (﹣
) B. (﹣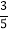 ,
,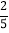 ) C. (﹣
) C. (﹣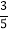 ,
,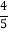 ) D. (﹣
) D. (﹣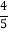 ,
,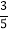 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤(a﹣2b+c)<0,其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍,乒乓球每盒定价5元,乒乓球拍每副定价20元.现两家商店都搞促销活动,甲店每买一副球拍赠一盒乒乓球;乙店按九折优惠.某班级需购球拍4副,乒乓球x盒(x≥4).
(1)若在甲店购买付款
 (元),在乙店购买付款
(元),在乙店购买付款 (元),分别写出与x的函数关系式;
(元),分别写出与x的函数关系式;(2)买30盒乒乓球时,在哪家商店购买合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

