【题目】为了抓住世博会商机,某商店决定购进A、B两种世博会纪念品,若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出4000元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B钟纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少?
参考答案:
【答案】
(1)
解:设购进A种纪念品每件需x元,B种纪念品每件需y元,
由题意得: ![]() ,解得
,解得 ![]() .
.
答:购进A种纪念品每件需50元,B种纪念品每件需100元.
(2)
解:设购进B种纪念品的数量为a件,则A种纪念品需要购进 ![]() =80-2a件,
=80-2a件,
由题意得:6a≤80-2a≤8a,
解得8≤a≤10.
因为a为整数,
所以a可取8,9,10,共有3种进货方案.
分别是:
方案一:购进A种64件,B种8件;
方案二:购进A种62件,B种9件;
方案三:购进A种60件,B种10件;
(3)
解:方案一:20×64+30×8=1520(元);
方案二:20×62+30×9=1510(元);
方案三:20×60+30×10=1500(元).
所以方案一获利最大,最大利润是1520元.
【解析】(1)根据题目中两个数量关系列二元一次方程组解答;(2)列不等式求解,设购进B种纪念品的数量为a件,所以A的件数为 ![]() ,即为
,即为 ![]() ,由6a≤A的件数≤8a,即可求出a的取值范围;(3)总利润=A种获利+B种获利=A种单件利润×A件件数+B种单件利润×B件件数.
,由6a≤A的件数≤8a,即可求出a的取值范围;(3)总利润=A种获利+B种获利=A种单件利润×A件件数+B种单件利润×B件件数.
【考点精析】解答此题的关键在于理解二元一次方程的解的相关知识,掌握适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解,以及对解二元一次方程组的理解,了解二元一次方程组:①代入消元法;②加减消元法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式3x≤2(x-1)的解集为( )
A. x≤-1 B. x≥-1 C. x≤-2 D. x≥2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x+y=7,x﹣y=4,则x2﹣y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形的三边为三个连续偶数,则它的三边长分别为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习了反比例函数,在生活中,两个变量间具有反比例函数关系的实例有许多,例如:在路程s一定时,平均速度v是运行时间t的反比例函数,其函数关系式可以写为:v=
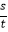 (s为常数,s≠0).
(s为常数,s≠0).
请你仿照上例,再举一个在日常生活、学习中,两个变量间具有反比例函数关系的实例:;并写出这两个变量之间的函数解析式: . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知α为锐角,且sinα=cosα,则α=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
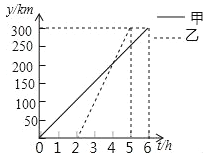
A.1个 B.2个 C.3个 D.4个
相关试题

