【题目】如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D. 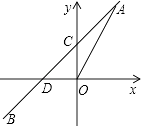
(1)m=;
(2)若一次函数图象经过点B(﹣2,﹣1),求一次函数的解析式;
(3)在(2)的条件下,求△AOD的面积.
参考答案:
【答案】
(1)1
(2)解:把(1,2)和(﹣2,﹣1)代入y=kx+b,得
![]() ,
,
解,得
![]() ,
,
则一次函数解析式是y=x+1
(3)解:令y=0,则x=﹣1.
则△AOD的面积= ![]() ×1×2=1
×1×2=1
【解析】解:(1)∵正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2), ∴2m=2,
m=1.
故答案为:1;
(1)根据正比例函数解析式求得m的值,(2)进一步运用待定系数法求得一次函数的解析式;(3)根据(2)中的解析式,令y=0求得点D的坐标,从而求得三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”黄金周期间,为了促销商品,甲、乙两个商店都采取优惠措施,甲店推出八折后再打八折,乙店则一次性六折优惠,若同样价格的商品,下列结论正确的是( )
A. 甲比乙优惠 B. 乙比甲优惠 C. 两店优惠条件相同 D. 不能进行比较
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县2018年元旦的最高气温为5℃,最低气温为﹣2℃,那么这天的最高气温比最低气温高_____℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为开展好大课间活动,欲购买单价为20元的排球和单价为80元的篮球共100个.
(1)设购买排球数为x(个),购买两种球的总费用为y(元),请你写出y与x的函数关系式(不要求写出自变量的取值范围);
(2)如果购买两种球的总费用不超过6620元,并且篮球数不少于排球数的3倍,那么有哪几种购买方案?
(3)从节约开支的角度来看,你认为采用哪种方案更合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】写出数轴上比-5大的所有负整数
-
科目: 来源: 题型:
查看答案和解析>>【题目】设一列数
 、
、 、
、 、…、 a2010中任意三个相邻数之和都是35,已知a3=2x,a20=15,
、…、 a2010中任意三个相邻数之和都是35,已知a3=2x,a20=15,  ,那么a2011=_________________。
,那么a2011=_________________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.
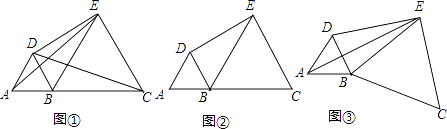
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数.
相关试题

