【题目】解下列分式方程
(1)![]() =
=![]() ; (2)
; (2) ![]() .
.
参考答案:
【答案】(1) x=9;(2)无解
【解析】
(1)方程两边同乘以最简公分母x(x-3),把分式方程转化为整式方程进行求解,然后把x的值代入到最简公分母进行检验,确定原方程的解;
(2)先把方程两边同时乘以(x+1)(x-1),求出x的值,代入最简公分母进行检验即可.
(1)方程两边同乘以最简公分母x(x-3)得:2x=3x-9,
整理的:x=9;
检验:当x=9时,x(x-2)=3×1=3≠0,
所以,x=9是原方程的解;
(2)方程两边同时乘以(x+1)(x-1)得,(x+1)2-4=x2-1,解得x=1,
检验:当x=1时,(x+1)(x-1)=(1+1)(1-1)=0,
故x=1是原分式方程的增根,原分式方程无解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
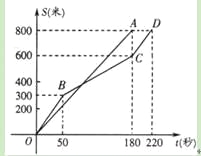
A. 小莹的速度随时间的增大而增大B. 小梅的平均速度比小莹的平均速度大
C. 在起跑后180秒时,两人相遇D. 在起跑后50秒时,小梅在小莹的前面
-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为2
 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.(1)连接CQ,证明:CQ=AP;
(2)设AP=x,CE=y,试写出y关于x的函数关系式,并求当x为何值时,CE=
 BC;
BC;(3)猜想PF与EQ的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.

(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的解析式为y=2x+5,其图象过点A(-2,a),B(b,-1).
(1)求a,b的值,并画出此一次函数的图象;(2)在y轴上是否存在点C,使得AC+BC的值最小?若存在,求出点C的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
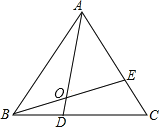
查看答案和解析>>【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.
相关试题

