【题目】小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁,图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
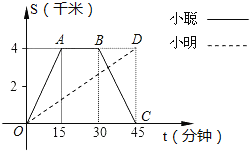
(1)小聪在天一阁查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
参考答案:
【答案】(1)15分钟,![]() 千米/分钟.(2)s=
千米/分钟.(2)s=![]() t(0≤t≤45).(3)当小聪与小明迎面相遇时,他们离学校的路程是3千米.
t(0≤t≤45).(3)当小聪与小明迎面相遇时,他们离学校的路程是3千米.
【解析】
试题分析:(1)直接根据图象上所给的数据的实际意义可求解;
(2)由图象可知,s是t的正比例函数,设所求函数的解析式为s=kt(k≠0),把(45,4)代入解析式利用待定系数法即可求解;
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设函数解析式为s=mt+n(m≠0)
把(30,4),(45,0)代入利用待定系数法先求得函数关系式,再根据求函数图象的交点方法求得交点坐标即可.
解:(1)∵30﹣15=15,4÷15=![]()
∴小聪在天一阁查阅资料的时间和小聪返回学校的速度分别是15分钟,![]() 千米/分钟.
千米/分钟.
(2)由图象可知,s是t的正比例函数
设所求函数的解析式为s=kt(k≠0)
代入(45,4),得
4=45k
解得k=![]()
∴s与t的函数关系式s=![]() t(0≤t≤45).
t(0≤t≤45).
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设函数解析式为s=mt+n(m≠0)
代入(30,4),(45,0),得
![]()
解得
∴s=﹣![]() t+12(30≤t≤45)
t+12(30≤t≤45)
令﹣![]() t+12=
t+12=![]() t,解得t=
t,解得t=![]()
当t=![]() 时,S=
时,S=![]() ×
×![]() =3.
=3.
答:当小聪与小明迎面相遇时,他们离学校的路程是3千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:①零是正数;②零是整数;③零是最小的有理数;④零是非负数;⑤零是偶数,正确命题的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正六边形的周长是12,则它的半径是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.

水银柱的长度x(cm)
4.2
…
8.2
9.8
体温计的读数y(℃)
35.0
…
40.0
42.0
(1)求y关于x的函数关系式(不需要写出函数的定义域);
(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)解题探究
已知三角形ABC,探究∠A+∠B+∠C等于多少度?(提示:过一点作平行线)

(2)发现规律
如图①,三角形ABC中,点D在BC的延长线上,试说明∠A+∠B与∠1的关系?

(3)运用规律
利用以上规律,快速探究以下各图:



当AB∥CD时,∠A,∠C,∠P的关系式为(直接填空,不要证明过程):
∠C = ,∠C = ,∠C =
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是一块锐角三角形余料,边BC=180mm,高AD=120mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
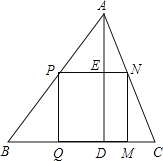
(1)若这个矩形是正方形,那么边长是多少?
(2)若这个矩形的长是宽的2倍,则边长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
已知,如图,BE平分∠ABC,CE平分∠BCD,且∠1+∠2=90,求证:AB∥CD.

证明:∵BE平分∠ABC. ( )
∴ . ( )
同理: .
∴∠ABC+∠BCD=2(∠1+∠2). ( )
∵ . ( )
∴ . ( )
∴AB∥CD. ( )
相关试题

