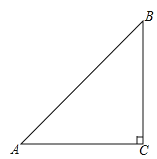
【题目】如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.
(1)(4分)用尺规作图,在CA的延长线上截取AD=AB,并连接BD(不写作法,保留作图痕迹);
(2)(4分)求∠BDC的度数;
(3)(4分)定义:在直角三角形中,一个锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即![]() ,根据定义,利用图形求cot22.5°的值.
,根据定义,利用图形求cot22.5°的值.
参考答案:
【答案】(1)答案见试题解析;(2)22.5°;(3)![]() .
.
【解析】
试题分析:(1)以点A为圆心,AB为半径作弧交CA的延长线于D,然后连结BD;
(2)由AD=AB得∠ADB=∠ABD,然后利用三角形外角性质可求出∠ADB=22.5°;
(3)设AC=x,根据题意得△ACB为等腰直角三角形,则BC=AC=x,AB=![]() ,所以AD=AB=
,所以AD=AB=![]() ,CD=
,CD=![]() ,在Rt△BCD中,根据余切的定义求解.
,在Rt△BCD中,根据余切的定义求解.
试题解析:(1)如图,

(2)∵AD=AB,∴∠ADB=∠ABD,而∠BAC=∠ADB+∠ABD,∴∠ADB=![]() ∠BAC=
∠BAC=![]() ×45°=22.5°,即∠BDC的度数为22.5°;
×45°=22.5°,即∠BDC的度数为22.5°;
(3)设AC=x,∵∠C=90°,∠BAC=45°,∴△ACB为等腰直角三角形,∴BC=AC=x,AB=![]() AC=
AC=![]() ,∴AD=AB=
,∴AD=AB=![]() ,∴CD=
,∴CD=![]() =
=![]() ,在Rt△BCD中,cot∠BDC=
,在Rt△BCD中,cot∠BDC=![]() =
=![]() =
=![]() ,即cot22.5°=
,即cot22.5°=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知1微米=10﹣7米,则25微米用科学记数法表示为( )
A.0.25×10﹣5米
B.25×10﹣7米
C.2.5×10﹣6米
D.2.5×10﹣8米 -
科目: 来源: 题型:
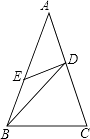
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组决定去市场购买A,B,C三种仪器,其单价分别为3元,5元,7元,购买这批仪器需花62元;经过讨价还价,最后以每种单价各下降1元成交,结果只花50元就买下了这批仪器.那么A种仪器最多可买( )
A.8件 B.7件 C.6件 D.5件
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);如图②,∠CBO=
 ∠ABC,∠BCO=
∠ABC,∠BCO= ∠ACB,∠A=α,则∠BOC= (用α表示)
∠ACB,∠A=α,则∠BOC= (用α表示)拓展研究:
(2)如图③,∠CBO=
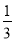 ∠DBC,∠BCO=
∠DBC,∠BCO=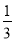 ∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=
 ∠DBC,∠BCO=
∠DBC,∠BCO= ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .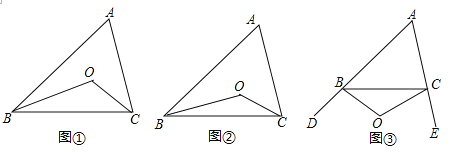
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
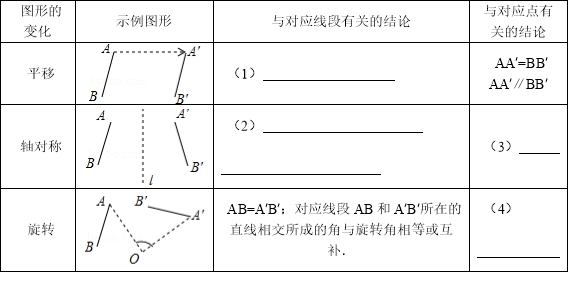
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
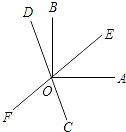
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
相关试题

