【题目】(10分)如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是 .
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,请说明理由.

参考答案:
【答案】(1)50°.(2)①6cm; ②存在,周长最小值为14cm
【解析】(1)50°.
(2)①∵AN=BN,
∴BN+CN=AN+CN=AC,
∵AB=AC=8cm,
∴BN+CN=8cm,
∵△NBC的周长是14cm.
∴BC=14﹣8=6cm.
②∵A、B关于直线MN对称,
∴连接AC与MN的交点即为所求的P点,此时P和N重合,
即△BNC的周长就是△PBC的周长最小值,
∴△PBC的周长最小值为14cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016四川省乐山市第16题)在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若
 ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数
 图象上点M的“可控变点”,则点M的坐标为 ;
图象上点M的“可控变点”,则点M的坐标为 ;(2)若点P在函数
 (
( )的图象上,其“可控变点”Q的纵坐标y′的取值范围是
)的图象上,其“可控变点”Q的纵坐标y′的取值范围是 ,则实数a的取值范围是 .
,则实数a的取值范围是 . -
科目: 来源: 题型:
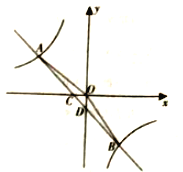
查看答案和解析>>【题目】(2016重庆市第22题)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与Y轴交于点D,点B的坐标为(m,-4),连接AO,AO=5,sin∠AOC=
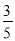 。
。(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程3ax﹣1=2a+x的解为1,则a的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)6(2ab+3a)-7(4a-ab)
(2)15o24′+32o47′-6o55′
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个有理数的平方等于它本身,那么这个有理数是( )
A. 0 B. 1 C. ±1 D. 0或1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3,…,均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2)…根据这个规律,点P2016的坐标为 .

相关试题

