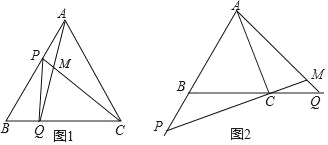
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)试求何时△PBQ是直角三角形?
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数.
参考答案:
【答案】(1)在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;(2)当t为![]() s或
s或![]() s 时,△PBQ为直角三角形;(3)在P、Q运动的过程中,∠CMQ的大小不变,∠CMQ=120°.
s 时,△PBQ为直角三角形;(3)在P、Q运动的过程中,∠CMQ的大小不变,∠CMQ=120°.
【解析】试题分析:(1)利用等边三角形的性质可证明△APC≌△BQA,则可求得∠BAQ=∠ACP,再利用三角形外角的性质可证得∠CMQ=60°;
(2)可用t分别表示出BP和BQ,分∠BPQ=90°和∠BPQ=90°两种情况,分别利用直角三角形的性质可得到关于t的方程,则可求得t的值;
(3)同(1)可证得△PBC≌△QCA,再利用三角形外角的性质可求得∠CMQ=120°.
试题解析:(1)∵△ABC为等边三角形,
∴AB=AC,∠B=∠PAC=60°,
∵点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
∴AP=BQ,
在△APC和△BQA中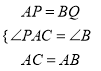 ,
,
∴△APC≌△BQA(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠CAQ+∠ACP=∠BAQ+∠CAQ=∠BAC=60°,
∴在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;
(2)∵运动时间为ts,则AP=BQ=t,
∴PB=4﹣t,
当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,
∴4﹣t=2t,解得t=![]() ,
,
当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2PB,
∴t=2(4﹣t),解得t=![]() ,
,
∴当t为![]() s或
s或![]() s 时,△PBQ为直角三角形;
s 时,△PBQ为直角三角形;
(3)在等边三角形ABC中,AC=BC,∠ABC=∠BCA=60°,
∴∠PBC=∠QCA=120°,且BP=CQ,
在△PBC和△QCA中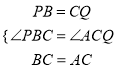 ,
,
∴△PBC≌△QCA(SAS),
∴∠BPC=∠MQC,
又∵∠PCB=∠MCQ,
∴∠CMQ=∠PBC=120°,
∴在P、Q运动的过程中,∠CMQ的大小不变,∠CMQ=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式3x﹣y+3的值是4,则多项式6x﹣2y的值是( )
A.0B.1C.2D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
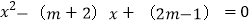 .
.(1)求证:方程恒有两个不相等的实数根 ;
(2)若此方程的一个根是1,请求出方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b互为相反数,c和d互为倒数,m是最大的负整数,则cd﹣a﹣b+m2019的值是( )
A.0B.﹣2C.﹣2或0D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】截止2019年10月30日,电影《我和我的祖国》的累计票房达到大约2560000000元,数据2560000000用料学记数法表示为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(a5)2=a10
B.x16÷x4=x4
C.2a2+3a2=6a4
D.b3b3=2b3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知空气的单位体积质量为1.24×10﹣3克/厘米3 , 1.24×10﹣3用小数表示为( )
A.0.000124
B.0.0124
C.﹣0.00124
D.0.00124
相关试题

