【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画.要求每位同学必须参加,且限报一项活动.以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图.请你结合图示所给出的信息解答下列问题. 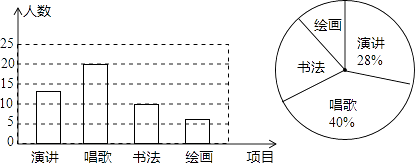
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
参考答案:
【答案】
(1)解:学生的总数是: ![]() ×100%=50(人),
×100%=50(人),
参加书法比赛的学生所占的比例是: ![]() ×100%=20%,
×100%=20%,
则参加绘画比赛的学生所占的比例是:1﹣28%﹣40%﹣20%=12%
(2)解:参加书法比赛的学生所占的比例是20%,
则扇形的圆心角的度数是:360×20%=72°
(3)解:参加演讲比赛的人数是:600×28%=168(人),
参加唱歌比赛的人数是:600×40%=240(人)
【解析】(1)各个项目的人数的和就是总人数,然后利用参加绘画比赛的学生数除以总人数即可求解;(2)利用对应的百分比乘以360度即可求解;(3)利用总人数600乘以对应的百分比即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.
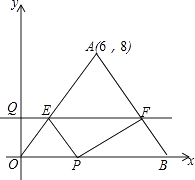
(1)求直线AB的解析式;
(2)若四边形POEF是平行四边形,求点P的坐标;
(3)是否存在点P,使△PEF为直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(﹣2,4),B(﹣2,1),C(﹣5,2).

(1)画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐同时乘以﹣2,得到对应的点A2 , B2 , C2 , 请画出△A2B2C2;
(3)则S△A1B1C1:S△A2B2C2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,与x轴交于点A(﹣2,0).

(1)求此二次函数的解析式;
(2)在抛物线上有一点P,满足S△AOP=1,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公司组织员工假期去旅游,租用了一辆耗油量为每百公里约为25L的大巴车,大巴车出发前油箱有油100L,大巴车的平均速度为80km/h,行驶若干小时后,由于害怕油箱中的油不够,在途中加了一次油,油箱中剩余油量y(L)与行驶时间x(h)之间的关系如图所示,请根据图象回答下列问题:

(1)汽车行驶h后加油,中途加油L;
(2)求加油前油箱剩余油量y与行驶时间x的函数解析式;
(3)若当油箱中剩余油量为10L时,油量表报警,提示需要加油,大巴车不再继续行驶,则该车最远能跑多远?此时,大巴车从出发到现在已经跑了多长时间? -
科目: 来源: 题型:
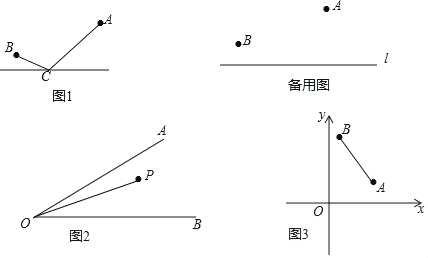
查看答案和解析>>【题目】唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望峰火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题我们称之为“饮马问题”.如图1所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河旁边的C点饮马后再到B点宿营.请问怎样走才能使总的路程最短?某课题组在探究这一问题时抽象出数学模型:
直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.
解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为线段A′B的长.
(1)根据上面的描述,在备用图中画出解决“饮马问题”的图形;
(2)利用轴对称作图解决“饮马问题”的依据是 .
(3)应用:①如图2,已知∠AOB=30°,其内部有一点P,OP=12,在∠AOB的两边分别有C、D两点(不同于点O),使△PCD的周长最小,请画出草图,并求出△PCD周长的最小值;
②如图3,点A(4,2),点B(1,6)在第一象限,在x轴、y轴上是否存在点D、点C,使得四边形ABCD的周长最小?若存在,请画出草图,并求其最小周长;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=60°,点E为直线AC上一点,D为直线BC上的一点,且DA=DE. 当点D在线段BC上时,如图①,易证:BD+AB=AE;
当点D在线段CB的延长线上时,如图②、图③,猜想线段BD,AB和AE之间又有怎样的数量关系?写出你的猜想,并选择一种情况给予证明.
相关试题

