【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD. 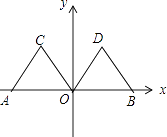
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△BOD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是度.
(2)连接AD,交OC于点E,求AD的长.
参考答案:
【答案】
(1)2;y轴;120
(2)解:如图,连接AD,
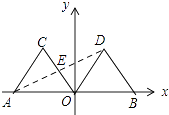
由AO=DO,∠BOD=60°可得,∠OAD=∠ODA=30°,
∴∠ADB=30°+60°=90°,
∴直角三角形ADB中,AD= ![]() =
= ![]() =2
=2 ![]() .
.
【解析】解:(1)△AOC沿x轴向右平移得到△OBD,根据AO=2可知,平移的距离是2个单位长度; △AOC与△BOD关于直线对称,根据线段AB被y轴垂直平分可知,对称轴是y轴;
△AOC绕原点O顺时针旋转得到△DOB,根据∠BOC=120°可知,旋转角度可以是120°;
所以答案是:2;y轴;120
【考点精析】本题主要考查了等边三角形的性质和坐标与图形变化-对称的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)才能正确解答此题.
-
科目: 来源: 题型:
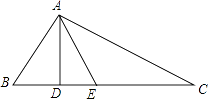
查看答案和解析>>【题目】如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC. 求证:E点在线段AC的垂直平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是随机事件的为 ( )
A. 一个图形旋转后所得的图形与原来的图形不全等
B. 元旦是晴天
C. y=(a+1)x+bx+c(a,b,c是常数)是二次函数
D. 在圆中任意画一个圆内接四边形,对角互补
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=-4x-2的截距是( )
A. 4 B. -4 C. 2 D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,若E、F分别是AB、AC上的点,且BE=AF.求证:△DEF为等腰直角三角形;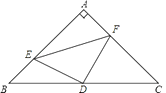
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程
 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个相似三角形的最短边分别为5cm和3cm,它们的周长之和为48cm,那么小三角形的周长为
A. 12cm B. 18cm
C. 24cm D. 30cm
相关试题

