搜索
【题目】如图，在△ABC中，AB=AC=5，P是BC边上除点B、C外的任意一点，则AP2+PBPC= ．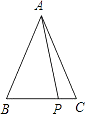 
参考答案：
【答案】25
【解析】解：过点A作AD⊥BC于D，
∵AB=AC=5，∠ADP=∠ADB=90°，
∴BD=CD，PA2=PD2+AD2 ， AD2+BD2=AB2 ，
∴AP2+PBPC=AP2+（BD+PD）（CD﹣PD）=AP2+（BD+PD）（BD﹣PD）=AP2+BD2﹣PD2=AP2﹣PD2+BD2=AD2+BD2=AB2=25．
故答案为25．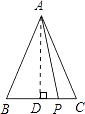
首先过点A作AD⊥BC于D，可得∠ADP=∠ADB=90°，又由AB=AC，根据三线合一的性质，可得BD=CD，由勾股定理可得PA2=PD2+AD2 ， AD2+BD2=AB2 ， 然后由AP2+PBPC=AP2+（BD+PD）（CD﹣PD），即可求得答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在正方形ABCD内有一点P，PA=3，PB=2，PC=1，求∠BPC的度数．
分析：根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′，这时再分别求出∠BP′P和∠AP′P的度数．
解答：（1）请你根据以上分析再通过计算求出图2中∠BPC的度数；
（2）如图3，若在正六边形ABCDEF内有一点P，且PA=2
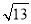，PB=4，PC=2，求∠BPC的度数．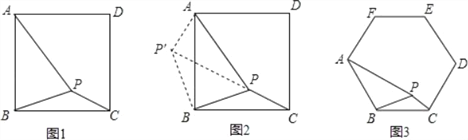
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：
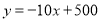．（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形纸片ABCD中，AB=6cm，AD=10cm，点E、F在矩形ABCD的边AB、AD上运动，将△AEF沿EF折叠，使点A′在BC边上，当折痕EF移动时，点A′在BC边上也随之移动．则A′C的取值范围为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若∠1＝∠2，则它们的补角____________（填“相等”，“不相等”，“无法确定”）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A，O，B三点在同一直线上，∠BOD与∠BOC互补．
（1）试判断∠AOC与∠BOD之间有怎样的数量关系，写出你的结论，并加以证明；
（2）OM平分∠AOC，ON平分∠AOD，①依题意，将备用图补全；
② 若∠MON=40°，求∠BOD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列成语描述的事件：①水涨船高；②守株待兔；③水中捞月；④缘木求鱼．其中为随机事件的是_____．
相关试题
