搜索
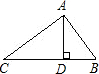
如图，在Rt△ABC中，AD⊥BC，已知△ACD的周长为32，△ABD的周长为24，则△ABC的周长为（ ）| A、50 | B、48 | C、44 | D、40 |
分析：在Rt△ABC中，AD⊥BC，易证得△ABD、△CAD、△CBA都相似．根据△ACD和△ABD的周长，可求出两三角形的相似比，也就求出了AB、AC的比例关系，可设未知数，分别表示出AB、AC、BC的长，进而可表示出AD、BD的长；然后可在△ABD中，根据△ABD的周长求出未知数的值，也就求出了AB、AC、BC的长，由此可求出△ABC的周长．
解答：解：∵在Rt△ABC中，AD⊥BC
∴∠CAB=∠CDA=90°，∠C=∠C
∴△ABC∽△DAC
同理得：△ABC∽△DBA
∴△ABC∽△DBA∽△DAC
∴
=
∵△ACD的周长为32，△ABD的周长为24
∴
=
=
=
∴设AB=3x，AC=4x
∴BC=5x，
∴
=
∴BD=
∵AD2+BD2=AB2，∴AD=
∴3x+
+
=24，∴x=
∴△ABC的周长为5x+4x+3x=12x=40．
故本题选D．
∴∠CAB=∠CDA=90°，∠C=∠C
∴△ABC∽△DAC
同理得：△ABC∽△DBA
∴△ABC∽△DBA∽△DAC
∴
| AB |
| BD |
| BC |
| AB |
∵△ACD的周长为32，△ABD的周长为24
∴
| △ABD的周长 |
| △ACD的周长 |
| 24 |
| 32 |
| 3 |
| 4 |
| AB |
| AC |
∴设AB=3x，AC=4x
∴BC=5x，
∴
| 3x |
| BD |
| 5x |
| 3x |
∴BD=
| 9x |
| 5 |
∵AD2+BD2=AB2，∴AD=
| 12x |
| 5 |
∴3x+
| 9x |
| 5 |
| 12x |
| 5 |
| 10 |
| 3 |
∴△ABC的周长为5x+4x+3x=12x=40．
故本题选D．
点评：此题考查了三角形的判定与性质、直角三角形的性质、方程思想等知识，综合性较强；解题时要细心求解．
